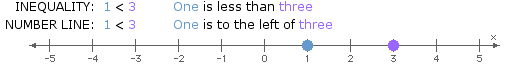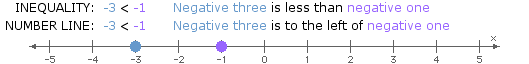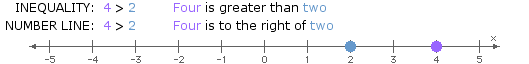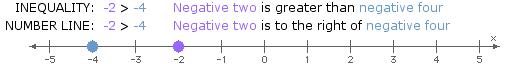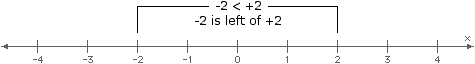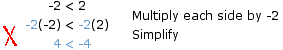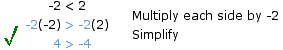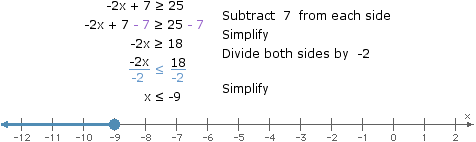An inequality is a mathematical relationship between two expressions and is represented using one of the following:
- ≤: "less than or equal to"
- <: "less than"
- ≠: "not equal to"
- >: "greater than"
- ≥: "greater than or equal to"

Inequalities involving "<", "≠" or ">" are referred to as "strict inequalities", while inequalities involving "≤" or "≥" are not.
If you "switch" the two sides of an inequality you must then reverse the direction of the inequality symbol. For example since it is true that 4 < 5, it is also true that 5 > 4.
An equation is a statement of equality between two expressions. An equation uses the equality symbol (=).
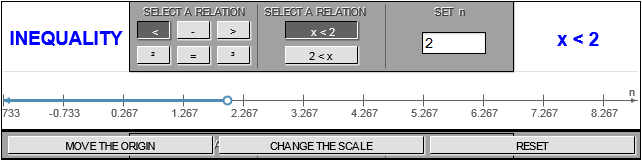
Like solutions to conditional equations, solutions to inequalities in one variable can be represented using a number line.
When considering locations along a number line, the inequality symbols can be interpreted as follows:
- ≤: "to the left of or coincidental with" or "to the left of including"
- <: "to the left of"
- ≠: "not coincidental with"
- >: "to the right of"
- ≥: "to the right of or coincidental with" or "to the right of including"
Strict inequalities are usually used when no variables are involved.
Inequalities involving a variable are sometimes referred to as "inequations".
At the present time, the term "inequality" refers to both inequations (with a variable) and simple inequalities without a variable.