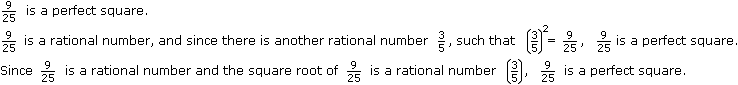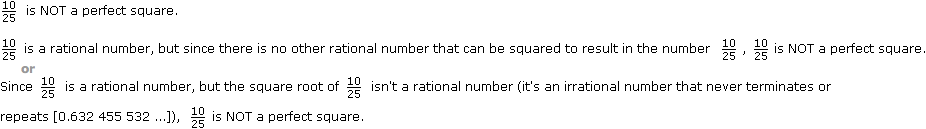A perfect square is a number, from a given number system, that can be expressed as the square of a number from the same number system.

25 is a perfect square.

25 is a natural number, and since there is another natural number 5, such that 5² = 25, 25 is a perfect square.

     or

Since 25 is a natural number and the square root of 25 is a natural number (5), 25 is a perfect square.

102.01 is a perfect square.

102.01 is a rational number, and since there is another rational number 10.1, such that (10.1)² = 102.01, 102.01 is a perfect square.

     or

Since 102.01 is a rational number and the square root of 102.01 is a rational number (10.1), 102.01 is a perfect square.

24 is NOT a perfect square.

24 is a natural number, but since there is no other natural number that can be squared to result in the number 24, 24 is NOT a perfect square.

     or

Since 24 is a natural number, but the square root of 24 isn't a natural number (it's an irrational number that never terminates or repeats [4.898 979 486 ...]), 24 is NOT a perfect square.

99.1 is NOT a perfect square.

99.1 is a rational number, but since there is no other rational number that can be squared to result in the number 99.1, 99.1 is NOT a perfect square.

     or

Since 99.1 is a rational number, but the square root of 99.1 isn't a rational number (it's an irrational number that never terminates or repeats [9.954 898 292 ...]), 99.1 is NOT a perfect square.