A relation is defined as a set of ordered pairs.
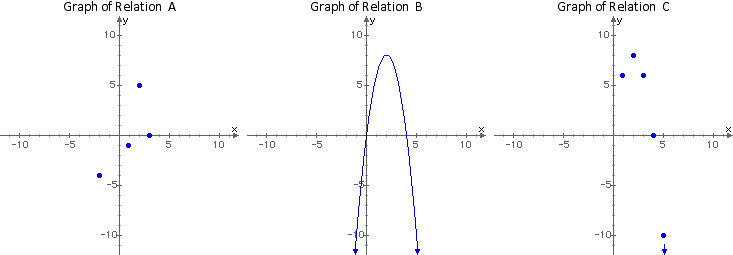
Relation A: { ( -2, -4 ), ( 1, -1 ), ( 2, 5 ), ( 3, 0 ) }
Relation B: { ( x, y ) | y = -2x2 + 8x }
Relation C: { ( x, y ) | y = -2x2 + 8x, x ∈ N }

When dealing with relations the Real numbers are assumed, unless otherwise stated (see Relation C).
Relations A, B and C are expressed using "set builder notation". Set builder notation is often used due to the definition of a relation as a "set of ordered pairs". Set builder notation usually begins with "{ ( x, y ) | ... }" (read as "The set of all ordered pairs x, y, such that ... "). Relations B and C are expressed below, without using set builder notation.
Relation B: y = -2x2 + 8x
Relation C: y = -2x2 + 8x, x ∈ N
Relation D: { ( ( y - 2 )2 - 9, y ) } or x = ( y - 2 )2 - 9
Relation E: { ( 2, y ) } or x = 2
Relation F: { ( x, y ) | ( x - 3 )2 + 4( y - 1 )2 ≤ 16 } or ( x - 3 )2 + 4( y - 1 )2 ≤ 16
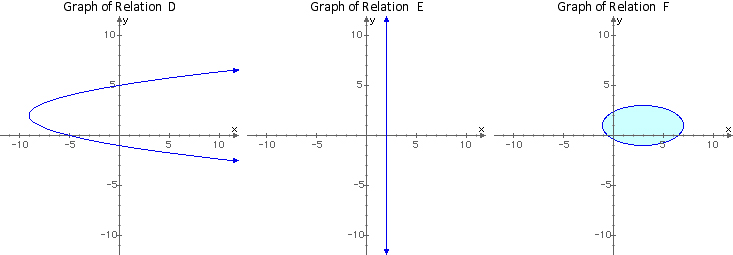
The first three relations (A, B and C) can also be classified as functions, whereas the last three relations (D, E and F) cannot.