It is important to be able to distinguish between terms like (-2)4 and terms like -24.
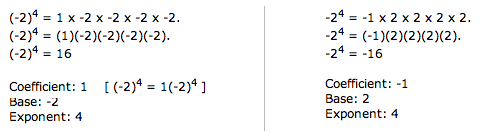
Note that is this case (-2)4 ≠ -24.
24 = 2 x 2 x 2 x 2.
24 = (2)(2)(2)(2).
24 = 16
Base: 2
Exponent: 4
Expanded Form: 2 x 2 x 2 x 2 or (2)(2)(2)(2).
Standard Form: 16
In the term 3(-2)5, 3 is a coefficient, (-2)5 is a power.
(-2)5 = -2 x -2 x -2 x -2 x -2.
(-2)5 = (-2)(-2)(-2)(-2)(-2).
(-2)5 = -32
3(-2)5 = 3 x -2 x -2 x -2 x -2 x -2.
3(-2)5 = (3)(-2)(-2)(-2)(-2)(-2).
3(-2)5 = -96
Coefficient: 3
Base: -2
Exponent: 5
Expanded Form: 3 x -2 x -2 x -2 x -2 x -2 or (3)(-2)(-2)(-2)(-2)(-2).
Standard Form: -96
In the term 5x4, 5 is a numerical coefficient, x4 is a power.
x4 = (x)(x)(x)(x).
5x4 = (5)(x)(x)(x)(x).
Numerical Coefficient: 5
Base: x
Exponent: 4
It is important to be able to distinguish between terms like (-2)4 and terms like -24.
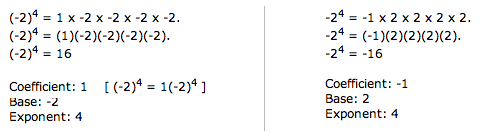
Note that is this case (-2)4 ≠ -24.
If a base is written without an exponent, the exponent is one.
 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.js