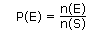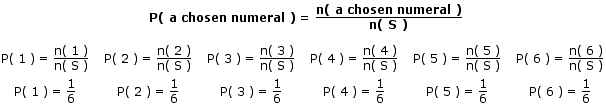Theoretical Probability
Definition
Probability is a value between (and including) zero and one.
If P(E) represents the probability of an event E, then:
A listing of all of the outcomes of an experiment is called the sample space (S) of the experiment and n(S) represents the number of outcomes in the sample space.
If n(E) represents the number of outcomes in event E, then in this context P(E) represents the theoretical probability that event E will occur and is given by:
Demonstration
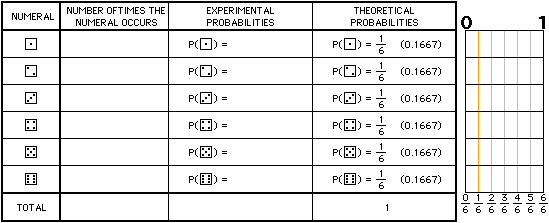
The more times the die is tossed, the closer the values of the experimental probabilities get to the values of the theoretical probabilities (of getting a chosen numeral).
Sample space (S) of throwing a die: { 1, 2, 3, 4, 5, 6 }
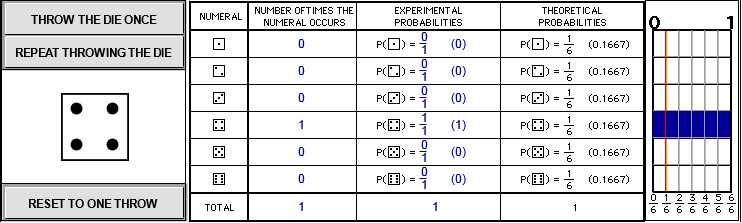 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.js
Demonstration
The more times the spinner is spun, the closer the values of the experimental probabilities get to the values of the theoretical probabilities (of landing in each sector).
Given each of the following:
- E: the event of the spinner stopping on sector E
- n(E): the size of central angle E
- S: the sample space of central angles
- n(S): the sum of the sizes of all of the central angles (360°)
- P(E): the probability of event E
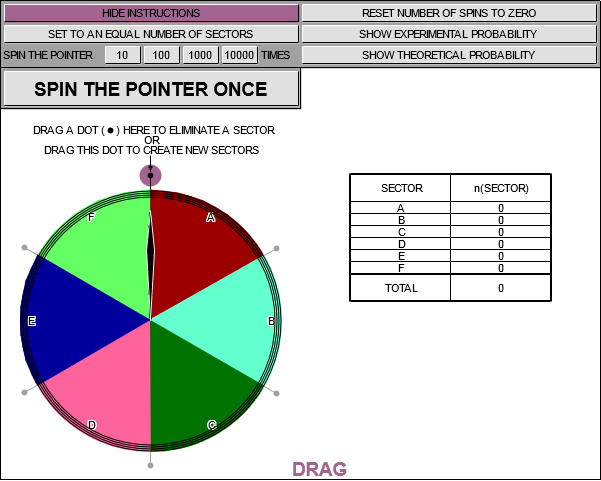 Image onlyInstructions text as in global.js
Image onlyInstructions text as in global.js