If "a" is a non-zero integer and "m" and "n" are whole numbers, then:
(am)n = amn
By the symmetric property of equality, this property can be written either way.
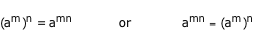
If "a" is a non-zero integer and "m" and "n" are whole numbers, then:
(am)n = amn
By the symmetric property of equality, this property can be written either way.
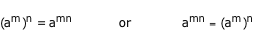
(23)4 = (23)(23)(23)(23) [Definition of a power]
(23)4 = (2x2x2)(2x2x2)(2x2x2)(2x2x2) [Definition of a power]
(23)4 = 2x2x2x2x2x2x2x2x2x2x2x2 [Definition of a power]
(23)4 = 212 [Definition of a power]

Generalization
(am)n = amn