Working with Linear Equations
Strand: Patterns and Relations (Variables and Equations)
Outcome: 3
Step 1: Identify Outcomes to Address
Guiding Questions
- What do I want my students to learn?
- What can my students currently understand and do?
- What do I want my students to understand and be able to do, based on the Big Ideas and specific outcomes in the program of studies?
 See Sequence of Outcomes from the Program of Studies
See Sequence of Outcomes from the Program of Studies
Big Ideas
Mathematics is sometimes referred to as the "science of patterns." Exploring patterns and then translating and representing these patterns into words, symbols, expressions, equations and graphs help Grade 9 students better understand linear functions. Connecting functions to prior learning and to real-life situations facilitates student learning. There are several important
Big Ideas that are addressed in this outcome:
- Algebra is a way to represent and explain mathematical relationships and is used to describe and analyze change (Small 2009, p.7).
- Equations are used to express relationships between two quantities (Van de Walle 2001, p. 384).
- The equal sign means that the quantity on the left-hand side of the equation is the same as the quantity on the right-hand side.
- A variable is a symbol that can stand for any one of a set of numbers or other objects and can be represented by boxes or letters (Van de Walle and Lovin 2006, p. 274).
 Grade 9
Grade 9








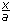 = b, a ≠ 0
= b, a ≠ 0 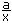 + b, x ≠ 0
+ b, x ≠ 0