Rational Numbers and Square Roots
Strand: Number
Outcomes: 3, 4, 5 and 6
Step 2: Determine Evidence of Student Learning
Guiding Questions
- What evidence will I look for to know that learning has occurred?
- What should students demonstrate to show their understanding of the mathematical concepts, skills and Big Ideas?
Using Achievement Indicators
As you begin planning lessons and learning
activities, keep in mind ongoing ways to monitor
and assess student learning. One starting point
for this planning is to consider the achievement
indicators listed in the Mathematics Kindergarten
to Grade 9 Program of Studies with Achievement
Indicators. You may also generate your
own indicators and use them to guide your observation
of the students.
The following indicators may be used to determine whether or not students have met the specific outcomes for understanding rational numbers. Can students:
- order a given set of rational numbers in fraction and decimal form by placing them on a number line; e.g.,
 , −0.666 … , 0.5, −
, −0.666 … , 0.5, −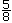 , −
, −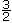 ?
?
- identify a rational number that is between two given rational numbers?
- solve a given problem involving operations on rational numbers in fraction or decimal form?
The following indicators may be used to determine whether or not students have met the specific outcome for applying the order of operations, including exponents to rational numbers. Can students:
- solve a given problem by applying the order of operations without the use of technology?
- solve a given problem by applying the order of operations with the use of technology?
- identify the error in applying the order of operations in a given incorrect solution?
The following indicators may be used to determine whether or not students have met the specific outcome for determining the square root of rational numbers that are perfect squares (principle square roots only). Can students:
- determine whether or not a given rational number is a square number, and explain the reasoning?
- determine the square root of a given positive rational number that is a perfect square?
- identify the error made in a given calculation of a square root; e.g., is 3.2 the square root
of 6.4?
- determine a positive rational number, given the square root of that positive rational number?
The following indicators may be used to determine whether or not students have met the specific outcome for approximating the square root of positive rational numbers that are not perfect squares. Can students:
- estimate the square root of a given rational number that is not a perfect square, using the roots of perfect squares as benchmarks?
- determine an approximate square root of a given rational number that is not a perfect square using technology; e.g., calculator, computer?
- explain why the square root of a given rational number, as shown on a calculator, may be an approximation?
- identify a number with a square root that is between two given numbers?
Sample behaviours to look for related to these
indicators are suggested for some of the activities
listed in Step 3, Section C:
Choosing Learning Activities.
 Grade 9
Grade 9






 , −0.666 … , 0.5, −
, −0.666 … , 0.5, −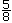 , −
, −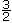 ?
?
