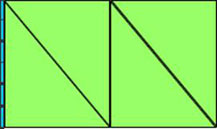
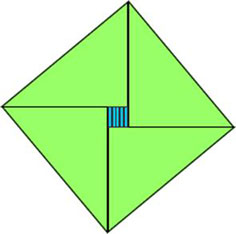
Building a Vibrant, Robust Mathematical Community

Knowledge of learning objectives from previous and following grades is necessary so teachers develop trajectories of learning that lead to conceptual growth and deepening of understandings. Complex mathematical concepts are well suited to problem and inquiry centred learning approaches, where students spend time constructing theories, models and experiments. An inquiry into areas of a geometric shape could have students finding, constructing and devising generalizations. For example:

A 3 × 5 index card has an area of 15 square units. You can see that the shape of this card is rectangular. If you want to create a square card with exactly the same area, 15 square units, the dimensions of the side will change. What this means is that the card has the same area as a square that also has 15 square units. It should be possible to cut up the 3 × 5 card into (several) pieces in such a way that these pieces can be put together to form a square card.

How can a square be constructed with sides that are the square root of 15, given only a 3 x 5 card? The card allows the measure of 3 units and 5 units easily. Put two cards together and 2 units can be measured off quite easily. But how can the square root of 15 units be measured?

Reproduced from Galileo Educational Network, "Area is a Square Deal," Galileo Educational Network, 2002–2007, www.galileo.org/math/investigations/area.html (Accessed August 8, 2007).

There are numerous tools that could be used for attempting to solve this problem: rulers, 3 × 5 index cards, scissors, grid paper and pencils. Computer aided manipulatives, like the geoboard from National Library of Virtual Manipulative at http://nlvm.usu.edu/en/nav/category_g_2_t_3.html, could be less cumbersome for students. One solution for the area is a square deal problem is shown below. There are other solutions to be found.

A robust mathematical community would strive for mathematical proficiency. Kilpatrick, Swafford and Findell (2001) define mathematical proficiency as having five intertwining strands:

conceptual understanding—an understanding of concepts, operations and relations. This frequently results in students comprehending connections and similarities to interrelated facts.
procedural fluency—flexibility, accuracy and efficiency in implementing appropriate procedures. Skill in proficiency includes the knowledge of when and how to use procedures. This includes efficiency and accuracy in basic computations.
strategic competence—the ability to formulate, represent and solve mathematical problems. This is similar to problem solving. Strategic competence is mutually supportive with conceptual understanding and procedural fluency.
adaptive reasoning—the capacity to think logically about concepts and conceptual relationships. Reasoning is needed to navigate through the various procedures, facts and concepts to arrive at solutions.
productive disposition—positive perceptions about mathematics. This develops as students gain more mathematical understanding and become capable of learning and doing mathematics.

Adapted from Jeremy Kilpatrick, Jane Swafford and Bradford Findell, Adding It Up: Helping Children Learn Mathematics (Washington, DC: National Academy Press, 2001), pp. 116, 118, 121, 124, 127, 129, 131.

Development of mathematical proficiency takes time. In each grade, students need to make progress along every strand mentioned above. Each strand is important and interwoven with the others.