Police :

Construction de figures

Télécharger la version imprimable

Résultat(s) d’apprentissage :

1re année, La forme et l’espace, n° 2, n° 3 2e année, La forme et l’espace, n° 6, n° 8 3e année, La forme et l’espace, n° 7

Matériel

Matériel Ciseaux Bâtons de colle Papier journal Carrés origami (ou autres patrons pliables de carrés) de deux couleurs différentes

Description :

Dans cette activité, les élèves construisent des figures en assemblant des triangles. Pour les élèves, le défi consiste à découvrir toutes les figures différentes qui peuvent être construites en respectant des règles. Chaque élève construit une figure et la colle sur du papier journal, puis tous les élèves trient leurs figures et discutent des similarités et des différences qu’ils observent en examinant ces figures. Ils essaient également de nommer chacune des figures qu’ils ont construites.

Activité

1. Montrez aux élèves comment plier un carré en diagonale et le découper pour obtenir deux triangles. Demandez-leur ensuite de le faire eux-mêmes en utilisant chacun un carré de l’une des deux couleurs.
2. Demandez-leur de déposer leurs deux triangles sur la table et de les utiliser pour construire une figure en suivant la règle. Expliquez-leur que la règle consiste à bien accoler leurs triangles en s’assurant que les côtés qui se touchent coïncident en entier, d’un coin à l’autre. Vous devrez modéliser l’application de cette règle pour que les élèves comprennent bien ce qui est accepté et ce qui ne l’est pas.
3. Demandez aux élèves de regarder les constructions de leurs compagnons de tablée pour voir combien de figures différentes ils ont faites.
   • Demandez à certains d’entre eux de venir devant la classe pour montrer leurs figures aux autres à l’aide du rétroprojecteur, et ce faisant, encouragez-les à nommer correctement leurs figures. Pour chacune des figures ainsi présentées, invitez tous les élèves de la classe qui ont construit la même de lever la main; et ainsi de suite... continuez de réclamer de la part des élèves qu’ils vous présentent toutes les figures différentes qu’ils ont trouvées. Et finalement, posez-leur la question suivante : Comment pouvez-vous savoir si vous avez trouvé toutes les figures qu’il était possible de construire avec vos triangles, tout en respectant notre règle? Les figures possibles (triangles, carrés et parallélogrammes) sont illustrées sous la rubrique Informations pour l’enseignant ci-dessus. Cela dit, rappelez-vous que, même si le terme parallélogramme n’est pas formellement inclus dans le plan de cours, il pourrait être intéressant d’en faire mention afin d’expliciter la distinction entre les quadrilatères et les carrés, étant donné que la définition des quadrilatères inclut la définition des carrés.
   Dans un groupe, on peut souvent s’attendre à ce que quatre figures différentes soient présentées et nommées, soit :
   • Le triangle...
   • Le parallélogramme...

   Mais il n’est pas impossible que la discussion mène les élèves à se demander s’il ne s’agit pas plutôt d’un losange, ce qui pourrait alors soulever quelques questions au sujet des propriétés de ces figures.  Par exemple : « Qu’est-ce que les losanges ont de particulier? », et « Bien... Et est-ce que la figure que nous avons ici a cette (ou ces) particularité? »

   • Le carré...
   • Le losange…

4. À l’aide du rétroprojecteur, présentez aux élèves le nouveau triangle qu’ils pourraient construire avec les deux triangles dont ils disposent au départ, puis demandez-leur de le faire eux-mêmes. Répétez cet exercice avec chacune des autres figures.
5. Dites aux élèves que, maintenant qu’ils connaissent bien la règle qu’ils doivent respecter pour joindre leurs triangles, ils vont pouvoir essayer de le faire en utilisant quatre triangles. Demandez à chacun des élèves de prendre un carré de la deuxième couleur et de le découper en deux triangles, de sorte qu’il ait maintenant quatre triangles de deux couleurs différentes. Demandez-leur ensuite de construire une figure avec leurs quatre triangles, puis de la coller sur une feuille de papier journal.
6. Invitez ensuite les élèves à prendre leurs figures et à se rassembler autour d’un espace inoccupé de la classe. Demandez-leur de disposer leurs figures par groupes, sur le sol (ou de les afficher sur un bout de mur totalement découvert), puis d’expliquer aux autres sur quoi ils se sont basés pour placer leur figure dans un groupe ou un autre. Cela fera sans doute ressortir les différences entre les divers hexagones et les pentagones réguliers ainsi que les hexagones et les pentagones irréguliers. Demandez ensuite aux élèves de trier de nouveau leurs figures, mais en se basant maintenant sur une règle différente que la première fois. Quoique l’enseignement des concepts d’hexagone et de pentagone outrepasse en partie le programme d’études antérieur à la 3^e année, le simple fait de trier différentes figures en se basant sur leurs ressemblances et leurs différences représente une expérience des plus enrichissantes pour les élèves. L’enseignement des termes pentagone et hexagone et de leur définition respective n’est toutefois pas nécessaire à ce stade.

Extension

Si la règle était modifiée de sorte que les élèves soient autorisés à joindre des côtés de figures sans que leurs extrémités coïncident, alors combien de figures différentes serait-il possible de construire?

Informations pour l’enseignant

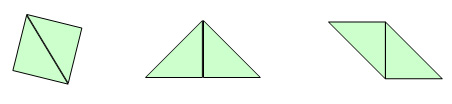
Les deux premiers triangles utilisés dans cette activité permettront aux élèves de construire trois figures en suivant les règles : un carré, un triangle et un quadrilatère (illustrés à la page suivante). Bien que cela ne soit pas prévu par le programme d’études de la 1^re à la 3^e année, les élèves aiment bien apprendre des « grands » mots, et tout particulièrement quand ceux-ci sont amusants à prononcer. Vous pourriez par exemple introduire le terme « parallélogramme », d’autant plus que ce terme permet de distinguer cette figure du carré, lequel est également un quadrilatère. Vous pourriez bien entendre vos jeunes élèves s’amuser à dire « para llélo llélo llélo gramme » juste pour le plaisir de s’entendre répéter les syllabes -llélo-.

À l’étape suivante de l’activité (point 5), les élèves utilisent un plus grand nombre de triangles (soit 4 triangles) de deux couleurs différentes pour construire des figures. Cela leur offre plus d’options, incluant la possibilité de construire des figures de la même forme mais de couleurs différentes, comme ci-dessous :

... ainsi que des figures de formes différentes.

Voici, par exemple, quatre hexagones différents

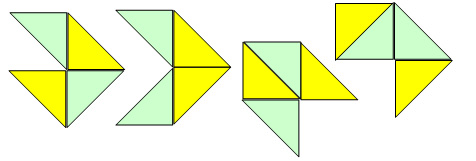
et un pentagone.

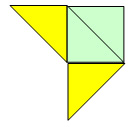
Remarque. – Vous devez vous attendre à ce que vos élèves soulèvent souvent des questions dont la portée dépasse celle des résultats d’apprentissage explicitement inclus dans le programme d’études correspondant à leur niveau scolaire. Ces sujets devraient tout de même être explorés au fur et à mesure qu’ils se présentent. Les élèves ont besoin d’expérimenter et de manipuler des idées au moment où celles-ci se présentent naturellement à leur esprit, même si cela leur arrive bien avant que nous attendions d’eux qu’ils s’y intéressent en raison des exigences prévues par leur programme d’études. Cependant, ces discussions, même si elles engagent toute la classe, ne devraient pas faire l’objet d’évaluation.

Les questions qui pourraient être soulevées lors de discussions incluent les suivantes :

• La symétrie : la symétrie pourrait être associée tant aux formes des figures qu’à leur(s) couleur(s). Aux yeux des enseignants (bien davantage que dans l’esprit des élèves), il existe une distinction entre la symétrie de réflexion et la symétrie de rotation. Les parallélogrammes, par exemple, seront utilisés pour illustrer la symétrie de rotation, et non la symétrie résultant d’une réflexion.
• La concavité : certaines des figures construites par les élèves seront concaves. Nous ne nous attendrons pas à ce que les élèves de la maternelle à la 3^e année emploient le terme concave, mais il n’en reste pas moins que les enseignants devraient être conscients de cette particularité.
• Les propriétés nécessaires pour définir une figure donnée.
• Les noms de différentes figures : trapézoïde ou trapèze, par exemple.

Demandez aux participants de vous proposer d’autres explorations possibles, lesquelles pourraient, par exemple, se formuler comme suit :

• Combien de figures différentes est-il possible de construire? et Que pouvons-nous faire pour vérifier si nous avons bien trouvé toutes les figures possibles?
• Et si nous tenions compte des couleurs différentes en plus des formes de nos figures, combien de figures différentes pourrions-nous construire?

Il est vraiment important d’offrir aux élèves de nombreuses occasions de consolider leur apprentissage en les conviant souvent à des discussions lors desquelles ils doivent centrer leur attention sur ce qu’ils ont appris pendant chacune des activités que nous leur proposons et en relever les principaux aspects.

L’une des principales questions qui devraient être soulevées dans le cadre de la présente activité est celle de la distinction entre les figures régulières et les figures irrégulières. Le carré est une figure parfaitement régulière, étant donné que tous ses côtés sont égaux et que tous ses angles le sont aussi. Par contre, les triangles que les élèves ont découpés et qu’ils ont utilisés pour construire leurs figures sont des triangles irréguliers, puisque leurs côtés ne sont pas tous d’égales longueurs et que leurs angles ne sont pas tous égaux. Bien que les triangles qu’ils ont construits soient symétriques (l’un par rapport à l’autre), le fait que chacun de ces triangles comporte des côtés et des angles inégaux nous force à conclure qu’il s’agit de figures irrégulières.

Les élèves (de même que les adultes...) ont trop souvent tendance à associer le nom d’une figure à l’image « régulière » de la figure désignée par ce nom. Cela aura par exemple pour conséquence que, lorsqu’ils seront exposés à des hexagones irréguliers, ils ne seront pas en mesure de constater qu’il s’agit tout de même d’hexagones. Il est donc important d’encourager les enseignants à discuter avec vous des caractéristiques des figures régulières (soit de l’égalité de leurs côtés et de leurs angles, par exemple); question qui peut s’étendre aux objets à trois dimensions, tels que les cinq polyèdres réguliers dont toutes les faces, toutes les arêtes et tous les sommets sont congruents.

Et dans le même ordre d’idée, la sphère est un objet particulièrement régulier, même s’il ne s’agit pas d’un polyèdre.

Source : Cartable Enseignement des concepts de mesure, M-3, Alberta Education, 2007.

Droit d’auteur  |  Rétroaction