Police :

De la réalité à l’équation

Télécharger la version imprimable

Résultat(s) d’apprentissage :

4e année, Les régularités et les relations, n° 5

Matériel

Matériel Ruban de caisse enregistreuse Ensembles de bandes de ruban de caisse enregistreuse de chacune des longueurs suivantes : 46 cm et 54 cm 48 cm et 52 cm 52 cm et 48 cm 56 cm et 44 cm Languettes adhésives Cubes emboîtables

Description :

Dans cette tâche, les élèves utilisent des modèles pour exprimer des problèmes de collection et de comparaison sous la forme d’équations. Ils explorent l’idée que les variables représentent des quantités spécifiques et inconnues. En interprétant des situations de la vie quotidienne et en utilisant la notation symbolique pour les modéliser, les élèves approfondissent leur compréhension des opérations d’addition et de soustraction qu’ils ont déjà explorées pendant les années antérieures de l’élémentaire. Ils font également un retour sur la signification du symbole d’égalité.

Activité

Partie 1 de l’activité :  Situations impliquant des relations partie-partie-tout ou des collections

1. L’enseignant donne à chaque élève une de ses bandes de ruban de caisse enregistreuse. Chaque élève mesure sa bande et en inscrit la longueur sur une languette adhésive qu’il colle sur sa poitrine. Le défi de chaque élève consiste à trouver un partenaire qui a une bande de ruban dont la longueur, une fois ajoutée à la longueur de la sienne, donnera une bande qui mesurera exactement 1 m.
2. Les élèves doivent élaborer des stratégies de calcul mental pour prédire la longueur que devra avoir la bande de leur partenaire. Et…, une fois leur partenaire trouvé, ils vérifient leur hypothèse en plaçant leurs bandes bout à bout et en les mesurant à l’aide d’un mètre.
3. Les élèves partagent ensuite les stratégies de calcul mental qu’ils ont utilisées pour trouver leur partenaire. Ils tracent également un dessin représentant la situation, en utilisant, par exemple, une ligne continue pour représenter leur propre bande et une ligne pointillée pour représenter celle de leur partenaire.



Relations partie-partie-tout ou collections Tout inconnu Marion a 15 billes rouges et 28 billes bleues. Combien de billes a-t-elle en tout? Partie inconnue Marion a 43 billes. Quinze d’entre elles sont rouges, et toutes les autres sont bleues. Combien de billes bleues Marion possède-t-elle?

Comparaisons Différence inconnue Marion a 15 billes rouges et 28 billes bleues. Combien de billes bleues a-t-elle de plus que de billes rouges? (Faites la comparaison.) Grande quantité inconnue Marion a 15 billes rouges et un certain nombre de billes bleues. En fait, elle a 13 billes bleues de plus que de billes rouges. Combien de billes bleues a-t-elle? Petite quantité inconnue Marion a 28 billes bleues, et elle a 13 billes bleues de plus que de billes rouges. Combien de billes rouges a-t-elle?

4. L’enseignant modélise cette relation partie-partie-tout en utilisant un diagramme en arbre.

   

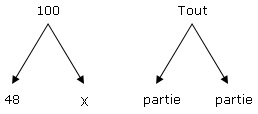
   	Résultat inconnu	Changement inconnu	Point de départ inconnu
   Problèmes reliés	Marion avait 15 billes, puis Juan lui en a donné 28 de plus. Combien de billes Marion a-t-elle en tout, maintenant?	Marion a 15 billes. Combien de billes de plus faudrait-il lui donner pour qu’elle en ait 43 en tout?	Marion avait quelques billes, puis Juan lui en a donné 15 de plus. Maintenant, Marion a 43 billes en tout. Combien de billes Marion avait-elle au départ?
   Problèmes indépendants	Marion avait 43 billes, puis elle en a donné 15 à Juan. Combien de billes reste-t-il à Marion maintenant?	Marion avait 43 billes, puis elle en a donné quelques-unes à Juan. Maintenant, il reste 15 billes à Marion. Combien de billes a-t-elle données à Juan?	Marion avait quelques billes, puis elle en a donné 15 à Juan. Maintenant, il reste 28 billes à Marion. Combien de billes Marion avait-elle au départ?

   Il montre ensuite aux élèves différentes façon d’écrire des équations pour représenter cette situation.

   48 + x = 100                     x + 48 = 100
   100 = x + 48                     100 = 48 + x

   Remarque. – Il est important que les élèves voient des équations dont les sommes/différences/produits/quotients apparaissent tant du côté droit que du côté gauche du symbole d’égalité.

5. L’enseignant soumet aux élèves d’autres problèmes du type partie-partie-tout, dans lesquels soit le tout soit l’une des parties est la valeur inconnue. Les élèves résolvent ces problèmes de façon concrète (matériel de manipulation) ou à l’aide de diagrammes (modèles).

Partie 2 : Situations de comparaison

• Cubes emboîtables (incluant des cubes blancs et de 2 autres couleurs)

1. L’enseignant soumet le problème suivant aux élèves.
   Marion a 15 billes rouges et 23 billes bleues. Combien de billes bleues a-t-elle de plus que de billes rouges?
2. Les élèves utilisent leurs cubes emboîtables pour modéliser cette situation : ils construisent 2 rangées de cubes, dont l’une représente les billes rouges et l’autre, les billes bleues. Pour déterminer la différence entre les 2 rangées, ils ajoutent des cubes blancs à la rangée rouge pour représenter la différence entre les 2 quantités.



3. Les élèves représentent cette situation en écrivant le plus grand nombre possible d’équations. Ils peuvent utiliser des figures ou des lettres comme variables.

   Pendant que les élèves partagent leurs équations, l’enseignant s’assure qu’ils ont envisagé un large éventail de possibilités, incluant des équations dont les sommes et les différences apparaissent tant à droite qu’à gauche du symbole d’égalité. Les élèves peuvent également utiliser des figures (ex. : des cubes blancs) ou des lettres différentes pour représenter la différence entre les 2 collections.

         

   15 + a = 23        23 = 15 + a        23 – a = 15        15 = 23 – a

   a + 15 = 23 23 = a + 15 23 – 15 = a a = 23 – 15

4. L’enseignant présente aux élèves un modèle qu’ils peuvent utiliser pour appuyer leur réflexion au sujet de problèmes de comparaisons similaires.



5. Les élèves résolvent d’autres problèmes de comparaisons dans lesquels soit la grande quantité, la petite quantité ou la différence sont utilisées comme variables. Les élèves alternent les types de symboles qu’ils utilisent comme variables.

Remarque. – Au début de l’élémentaire, les élèves ont déjà travaillé avec des variables (spécifiques et inconnues) pour résoudre des problèmes reliés et des problèmes indépendants.

Source : Patterns and Pre-Algebra, Gr. 4-6, Alberta Education, 2007. Activité traduite du cartable publié en anglais.

Droit d’auteur  |  Rétroaction