Activité
- L’enseignant raconte à haute voix le conte traditionnel chinois suivant :
Cette histoire est basée sur un conte traditionnel chinois
Un beau matin, le pauvre et vieux Monsieur Haktak trouve dans son jardin une énorme marmite en laiton très spéciale. Bien qu’il ne sache absolument pas à quoi elle pourrait bien servir, il décide de l’emporter chez lui. Il met sa bourse (et donc, toutes les pièces d’or qu’il lui reste) dans la marmite, puis il prend la marmite à deux mains et la transporte jusqu’à sa maison.
Un peu plus tard, Madame Haktak perd une de ses épingles à cheveux, alors qu’elle est penchée au-dessus de la marmite parce qu’elle espère bien découvrir ce qu’il y a dedans… Ce qui fait que son épingle à cheveux tombe dans la marmite!
Quand Madame Haktak plonge ensuite sa main dans la marmite pour récupérer son épingle à cheveux, le pouvoir magique de la marmite lui est révélé : non seulement la bonne dame y trouve-t-elle 2 épingles à cheveux identiques à celle qu’elle a perdue, mais en plus, elle y trouve deux bourses qui contiennent des pièces d’or – ce qui fait que Monsieur Haktak a maintenant deux fois plus de pièces d’or qu’avant!
Les Haktak sont évidemment enchantés, car ils réalisent bien vite qu’ils pourront désormais avoir 2 de tout ce qu’ils désirent, et qu’ils ne seront donc plus jamais pauvres. Toutefois, le sort tourne à leur désavantage le jour où Monsieur et Madame Haktak tombent tous les deux dans la marmite et doivent ensuite faire face à des doubles d’eux-mêmes!
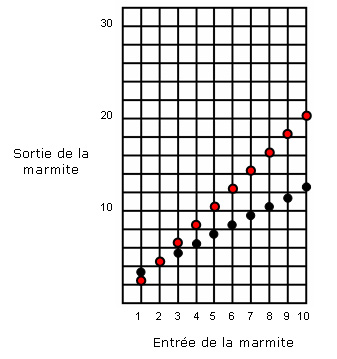
- Ensuite, les élèves testent deux autres marmites magiques : une qui ajoute chaque fois 2 pièces d’or à celles qui sont jetées dans la marmite, et une qui multiplie chaque fois par 2 le nombre de pièces d’or qui sont jetées dans la marmite.
- Les élèves utilisent des blocs de base dix pour tester ces 2 règles différentes (Ajouter 2, Multiplier par 2) et inscrivent leurs résultats dans un tableau d’entrées et de sorties.
- Les élèves de 6e année tracent les graphiques de ces deux différents modèles de croissance à l’intérieur d’un même plan cartésien. Chaque point (paire de coordonnées) représente une paire de valeurs d’entrée et de sortie correspondantes.
- En groupes, les élèves discutent afin de répondre à quelques questions, telles que :
- Quand est-il plus avantageux d’ajouter 2 que de multiplier par 2?
- Quand l’ajout de 2 donne-t-il le même résultat (la même sortie) que la multiplication par 2?
- Quand est-il plus avantageux de multiplier par 2?
- Laquelle des deux marmites préféreriez-vous posséder? Pourquoi?
- Les élèves comparent d’autres marmites dont les règles sont différentes des précédentes (ajouter 10 versus multiplier par 5, par exemple).
| Ajouter 2 | Multiplier par 2 |
 |
 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
Informations pour l’enseignant
Dans le tableau des multiplications cumulatives, chaque sortie est égale à 2x, où x représente le numéro de l’essai (soit le nombre d’utilisations successives de la marmite).
Remarque. – Il doit être clair que nous n’attendons pas des élèves du niveau élémentaire qu’ils expriment symboliquement cette relation sous la forme d’une expression.
Source : Patterns and Pre-Algebra, Gr. 4-6, Alberta Education, 2007. Activité adaptée du cartable publié en anglais.








