Activité
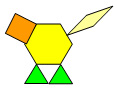
- L’enseignant construit un patron représentant l’iguane nouveau-né à l’aide de blocs projetables sur un rétroprojecteur. Les élèves essaient de deviner de quel type d’animal il s’agit.
- À côté du premier, l’enseignant construit ensuite le patron représentant l’iguane à l’âge de 1 an.
- Les élèves discutent ensemble de ce qui a changé et de ce qui n’a pas changé (soit la tête, les 2 pattes et le tronc) en passant d’un stade de développement à l’autre. Ensuite l’enseignant leur demande ce qui a varié (la queue s’est allongée de 1 bloc).
Remarque. – En employant le verbe varier en contexte, l’enseignant peut familiariser les élèves avec ce terme, lequel est relié au terme variable. Les élèves apprennent ainsi que la variable est la partie du patron qui change.
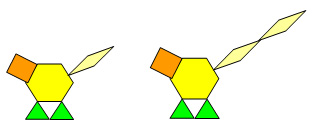
- À l’aide de blocs-formes, les élèves construisent les patrons représentant les 5 premiers stades de développement de l’iguane. Pendant qu’ils travaillent, l’enseignant les invite à identifier les éléments qui ne changent pas et ceux qui varient. Il les invite également à se demander quel est le lien entre le numéro de chaque stade de développement et le nombre de blocs inclus dans la queue de l’iguane à ce stade.
- Les élèves inscrivent leurs résultats dans un tableau, tout en remarquant que les parties du corps demeurent toujours pareilles et de quelle façon la longueur de la queue varie.
- Par écrit, les élèves expliquent quel nombre de blocs sera, selon eux, nécessaire pour construire un iguane au stade 10 et un iguane au stade 100, sans les dessiner ou les représenter à l’aide de blocs.
- Les élèves généralisent la régularité en expliquant par écrit comment ils pourraient déterminer le nombre total de blocs nécessaires pour représenter un iguane de n’importe quel âge (ou à n’importe quel stade de son développement).
- L’enseignant peut expliquer que le nombre de parties du corps qui ne change pas (soit le nombre 4) s’appelle une constante et que le nombre qui change (la longueur de la queue) est appelé une variable.
N° du stade de développement |
Corps + Queue |
Nombre total de blocs |
1 |
4 + 1 |
5 |
2 |
4 + 2 |
6 |
3 |
4 + 3 |
7 |
4 |
4 + 4 |
8 |
5 |
4 + 5 |
9 |
Extension
Les élèves construisent leurs propres régularités en créant, à l’aide de blocs-formes, des patrons représentant des animaux de leur choix ainsi que leur développement à différents stades de leur croissance. Pour chaque stade, ils consignent dans un tableau ce qui n’a pas changé depuis le stade précédent (la constante) et ce qui a changé (la variable). Ils mettent ensuite leurs camarades au défi de prédire combien de blocs seraient nécessaires pour représenter leur animal à son 10e et à son 100e stade de développement. Ensemble, les élèves peuvent formuler par écrit une généralisation qui leur permettrait de prédire combien de blocs seraient nécessaires pour représenter n’importe quel stade de développement.
Chenilles

N° du stade de développement |
Tête + Corps |
Nombre total de blocs |
1 |
3 + 2 |
5 |
2 |
3 + 4 |
7 |
3 |
3 + 6 |
9 |
4 |
3 + 8 |
11 |
5 |
3 + 10 |
13 |
Poissons

N° du stade de développement |
Tête + Corps + Queue |
Nombre total de blocs |
1 |
2 + 0 + 1 |
3 |
2 |
2 + 1 + 1 |
4 |
3 |
2 + 2 + 1 |
5 |
4 |
2 + 3 + 1 |
6 |
5 |
2 + 4 + 1 |
7 |
Informations pour l’enseignant
Les élèves apprennent comment des régularités qui comportent une constante peuvent être créées en effectuant des changements de façon systématique. Ils utilisent du matériel de manipulation pour découvrir ce qui change (varie) et ce qui demeure inchangé lors de la création d’une régularité qui représente un phénomène de croissance.
Source : Patterns and Pre-Algebra, Gr. 4-6, Alberta Education, 2007. Activité traduite du cartable publié en anglais.








