Police :
Résultat(s) d’apprentissage :
  • 6e année, Les régularités et les relations, n° 5
Matériel

Matériel

  • Accès à Internet pour utiliser un applet d’une balance à plateaux.
  • Balances mathématiques ou à plateaux (optionnel)
  • Photocopies de la fiche reproductible : « L’égalité »
    (1 par équipe)
  • Matériel de manipulation
Description : Les élèves explorent le concept de l’égalité à l’aide d’un applet de balance à plateaux.

Activité

  1. Amorcez la leçon en écrivant le symbole égal au tableau puis demandez aux élèves de vous dire ce que ce symbole veut dire pour eux.
  2. Notez les réponses des élèves au tableau puis proposez-leur de jouer à un jeu où ils devront maintenir l’égalité de chaque côté du symbole égal.
  3. Pour cette activité, les élèves ont besoin d’avoir accès à Internet afin d’utiliser un applet. Si vous n’avez pas accès à Internet, veuillez consulter la section Variante afin d’obtenir d’autres pistes d’exploration pour cette leçon.
  4. L’activité se déroule d’abord en salle de classe.
  5. En équipes de 2, les élèves débutent en écrivant une opération de départ dans la colonne de gauche de la première section de la fiche reproductible.
  6. Il peut s’agir d’une addition, d’une multiplication, d’une soustraction ou d’une division; c’est aux élèves de décider. Ils pourraient par exemple écrire l’équation suivante :


    7. Équation de départ Possibilités pour maintenir l’égalité

    1

    64 ÷ 8

    =
     1.
     2.
     3.
     4.
     5.
     6.
     7.
     8.
     9.
     10.

  7. Maintenant, ils doivent trouver le quotient de leur équation, puis penser à une autre équation qui permettrait de maintenir l’égalité, donc qui aurait aussi 8 comme réponse.
  8. Demandez aux élèves d’explorer à l’aide de matériel de manipulation et de noter un maximum de 10 possibilités différentes pour maintenir l’égalité.
  9. Pendant que les élèves travaillent, circulez et demandez-leur :
    • Comment faites-vous pour trouver des équations? En quoi le matériel de manipulation vous aide-t-il? Utilisez-vous des stratégies de calcul mental pour trouver des équations? Quelle stratégie utilisez-vous? Je remarque que vous avez beaucoup (nommez l’opération), pourquoi selon vous?
  10. Une fois les égalités trouvées, les élèves pourraient aller vérifier leurs réponses à l’aide de l’applet.
  11. L’applet permet de voir la réponse qui change au fur et à mesure que la quantité change. L’applet* est en anglais, mais comporte très peu de texte.

*Source : Tiré du site Web : <http://illuminations.nctm.org/ActivityDetail.aspx?ID=26> (dernier accès, le 2 février 2010).

  1. Voici un exemple de l’applet représentant l’équation de départ et 10 possibilités pour maintenir l’égalité.

    2. Équation de départ Possibilités pour maintenir l’égalité

    1

    64 ÷ 8

    =
     1.
     2.
     3.
     4.
     5.
     6.
     7.
     8.
     9.
     10.    		  4 + 4
     1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
     5 + 3
     3 + 3 + 2
     9 – 1
     16 – 8
     28 – 20
     18 – 10
     2 x 4
     1 x 1 x 1 x 2 x 2 x 2
  1. Si le temps le permet, les élèves pourraient recommencer avec une autre équation.
  2. Pour clore la leçon, demandez aux élèves de relire ce qu’ils vous avaient dit au début à propos de l’égalité. Demandez-leur si certains d’entre eux ont changé d’idée et si oui d’expliquer pourquoi. Ils pourraient écrire leurs découvertes dans leur journal de mathématiques.

Variante 1

Les élèves peuvent utiliser des balances mathématiques.

Les nombres possibles sont plus petits, mais les 4 opérations sont tout de même possibles. Ce type de balance pourrait convenir aux élèves qui ne se sentent pas à l’aise avec les plus grands nombres.

Variante 2

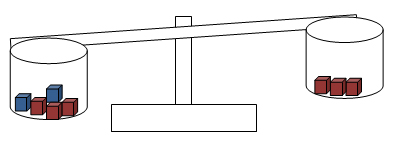
Les balances à plateaux peuvent aussi être utilisées. Il suffirait de représenter les quantités voulues de chaque côté sur une table avec du matériel de manipulation, devant la balance, puis de mettre le matériel dans les plateaux afin de voir si la balance est en équilibre. Ce type de balance permet de bien voir si l’égalité est maintenue de chaque côté. Les nombres possibles sont limités par la grosseur des contenants de chaque côté.

Variante 3

Pour augmenter le niveau de difficulté de l’activité, permettez aux élèves d’intégrer des opérations sur les plus grands nombres, les nombres décimaux ou sur les priorités des opérations.