Activité
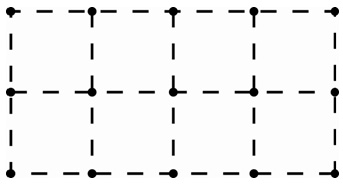
- Demandez aux élèves de tracer un rectangle de 2 x 4 sur leur papier à point ou leur géoplan. À partir de celui-ci, demandez-leur de trouver l’aire du rectangle. Invitez les élèves à expliquer comment ils trouvent l’aire et à prouver que l’aire est effectivement de 8 unités carrées.
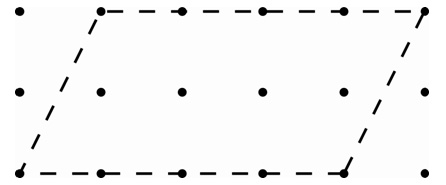
- Invitez ensuite les élèves à tracer un parallélogramme en déplaçant la ligne du haut du parallélogramme d’un point. En équipes de 2, ils essaient de trouver l’aire du parallélogramme. Ils compteront les unités carrées.
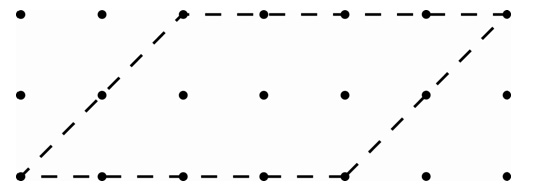
- Invitez ensuite les élèves à tracer un parallélogramme en déplaçant la ligne du haut du parallélogramme d’un autre point. Le nouveau parallélogramme est maintenant 2 points plus loin que le rectangle. En équipes de 2, ils essaient de trouver l’aire du parallélogramme.
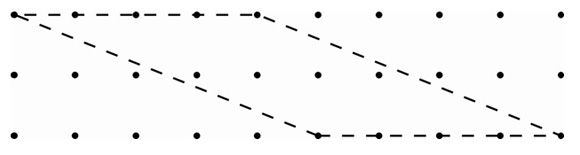
- Invitez les élèves à faire un nouvel essai avec de nouveaux parallélogrammes dont la ligne du haut s’éloigne de plus en plus de la ligne de la base (mais en demeurant toujours à la même hauteur). Les élèves devraient aussi tenter de revenir sur leurs pas et de faire pencher le rectangle de l’autre côté.
- Éventuellement, certains élèves feront remarquer que l’aire de tous les parallélogrammes ainsi créés est égale à l’aire du rectangle de départ. Assurez-vous que tous les élèves peuvent trouver la hauteur du parallélogramme et faire le lien entre celle-ci et le côté vertical du rectangle.
- Recommencez l’activité avec un autre rectangle, disons de 3 x 5 unités. Créez autant de parallélogrammes que possible et vérifiez l’aire.
- Concluez l’activité en écrivant une manière de trouver l’aire des parallélogrammes. Il est important d’utiliser les mots des élèves pour créer la formule. S’ils créent des formules qui ne sont pas justes, faites-les tester par les élèves pour leur permettre d’ajuster leur raisonnement.
Informations pour l’enseignant
La plupart des élèves savent trouver l’aire d’un rectangle. Il est important de retourner en arrière pour s’assurer qu’ils savent pourquoi et comment on en est venu à la formule de largeur x longueur avant de les mettre au défi de créer une formule pour trouver l’aire des parallélogrammes, des triangles ou des cercles.








