Activité
- Demandez aux élèves ce que veut dire selon eux « 50 % de la classe de Marie-Louise sont des garçons ». Est-ce qu’il y a 100 personnes dans sa classe? (Non, probablement pas.) Combien de personnes y a-t-il dans sa classe? (On ne le sait pas avec un pourcentage.) Combien de filles y a-t-il dans sa classe? (50 %, mais on ne le sait pas en nombre.)
- Montrez aux élèves une pièce de 1 $ et deux pièces de 25 ¢. Demandez-leur si 50 ¢ est 50 % de 1 $. Permettez-leur de donner leurs idées.
- Montrez ensuite une seule pièce de 25 ¢ et la pièce de 1 $ et demandez-leur quel pourcentage de 1 $ représente le 25 ¢? Faites de même avec 75 ¢ et avec 1 ¢.
- Faites le lien entre 50 ¢, 50 % et la moitié d’un nombre ou
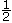, de même qu’avec 75 ¢ et 75 % et 
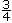et 25 ¢, 25 % et 
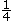. Discutez avec eux de la signification de 100 % et de 0 %. - Posez la question suivante aux élèves : Avez-vous un chien à la maison? Demandez-leur de répondre par oui ou par non. Au lieu de demander à chaque personne de répondre à tour de rôle à haute voix, demandez-leur de se placer des deux côtés de la classe; par exemple, tous ceux qui ont un chien se placent à droite de la classe et ceux qui n’en n’ont pas se placent à gauche. Debout, les élèves observent combien ils sont dans chaque groupe. Écrivez au tableau le nombre d’élèves qui ont un chien et ceux qui n’en n’ont pas. Demandez aux élèves de venir se rasseoir.
- Sur la fiche reproductible Tableau de fractions, demandez aux élèves de colorier (ou hachurer) la fraction des élèves qui ont répondu oui et celle qui ont répondu non. Il faudra qu’ils divisent le rectangle en parties selon le nombre d’élèves de la classe.
- Demandez aux élèves d’estimer le pourcentage de personnes qui ont un chien dans la classe et le pourcentage de personnes qui n’en ont pas. Est-ce que les deux pourcentages devraient être 100 %? Pourquoi?
- Invitez les élèves à placer un transparent du Tableau de pourcentages par-dessus leur fraction dessinée sur le Tableau de fractions. Ainsi, ils pourront constater le lien entre la fraction des élèves et son pourcentage correspondant.
- Montrez comment un pourcentage est une image toujours divisée en 100 parties d’un ensemble. Certains élèves feront peut-être le lien entre les fractions équivalentes.
- À l’aide d’une autre fiche reproductible, Tableau de fractions, demandez aux élèves de préparer une autre question pour laquelle ils feront un dessin des fractions correspondantes et calculeront les pourcentages. Par exemple, quel pourcentage des élèves de la classe portent des jeans? Quel pourcentage des élèves de la classe ont les cheveux blonds? Quel pourcentage des filles de la classe ont les ongles peints? Quel pourcentage des garçons de la classe portent des lunettes?
- Les élèves présentent leur pourcentage à la classe.
Informations pour l’enseignant
Cette activité pourrait bien se faire au tout début des leçons sur les pourcentages. Il n’y a pas de calcul formel des pourcentages, seulement un fondement pour bien comprendre le concept et le lier aux connaissances antérieures sur la monnaie et sur les fractions.
