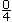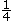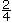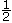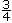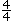Police :
Résultat(s) d’apprentissage :
  • 7e année, La statistique et la probabilité, n° 4
Matériel

Matériel

  • La météo du matin incluant un pourcentage de pluie, de soleil ou de neige
  • Deux copies de la fiche reproductible : « Cartes à jouer de 1 à 10 », de deux couleurs différentes, pour chaque élève
Description : À partir d’un jeu de cartes, les élèves font la liste de toutes les possibilités de résultats (l’espace échantillon) et verbalisent les probabilités des résultats. Ensuite, ils calculent les résultats théoriques et communiquent leurs probabilités sous différentes formes (fractions, nombres décimaux et pourcentages).

Activité

  1. Annoncez à la classe le pourcentage de possibilité de pluie (ou de neige) qui a été annoncée dans les nouvelles. Discutez de ce qu’un pourcentage de chance veut dire.
  2. Les élèves sont en équipes de 2. Invitez-les à jouer au 9 : deux cartes (une de chaque couleur) sont placées face fermée devant l’élève. L’élève regarde ses cartes et fait la somme des 2 cartes. Si un élève réussit à faire exactement la somme de 9, il gagne un point.
  3. Permettez aux élèves de jouer le jeu pendant quelques minutes, pour vous assurer que tout le monde le comprend bien.
  4. Arrêtez le jeu et demandez aux élèves en équipe de décrire l’espace échantillon de ce jeu. Discutez des diverses stratégies qui peuvent être employées pour décrire toutes les possibilités de résultats.

    5. Description de l’espace échantillon du jeu de 9

  5. Invitez les élèves à verbaliser la probabilité d’obtenir une somme de 9, selon la liste suivante. Faites des exemples de sommes impossibles et de résultats certains. Par exemple, il serait impossible d’obtenir une somme de 30 avec 2 cartes. Il est certain d’obtenir une somme positive avec deux cartes, car les nombres sont positifs.

    6. Impossible

    Moins probable

    Équiprobable

    Plus probable

    Certain

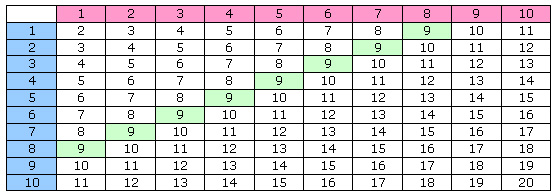
  6. Faites la comparaison entre l’espace échantillon et un entier. Dans ce jeu, l’espace échantillon comprend 100 résultats possibles. Le nombre de fois qu’on peut obtenir le résultat désiré, une somme de 9, correspondra au numérateur. Donc, on peut construire une fraction. Cette fraction est une « probabilité théorique ».
  7. Montrez aux élèves comment écrire cette probabilité théorique :

    8. P (somme de 9) = 8/100

  8. Indiquez aux élèves qu’on peut réduire cette fraction à sa plus simple expression = 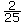2/25, comme on le fait avec toutes les fractions. De plus, on pourrait la changer à une décimale équivalente et à un pourcentage équivalent.
  9. En utilisant un tableau comme celui-ci, demandez aux élèves de faire des commentaires sur la probabilité d’obtenir 9 à ce jeu.

    10. Mot

    Fraction

    Décimale

    Pourcentage

    Impossible

    0/4

    0

    0 %

    Moins probable

    1/4

    0,25

    25 %

    Équiprobable
    2/4  =  1/2

    0,5

    50 %

    Plus probable

    3/4

    0,75

    75 %

    Certain

    4/4

    1

    100 %

  10. En équipes de 2, invitez les élèves à faire des modifications au jeu de manière à changer la probabilité de réussite des 2 joueurs. Demandez aux élèves d’expérimenter leur jeu avec les modifications voulues.
  11. Incitez les élèves à faire des espaces échantillons qui sont plus petits en enlevant des cartes. Trouvez la probabilité théorique de ces nouveaux jeux. Exprimez cette probabilité en pourcentage.