Activité
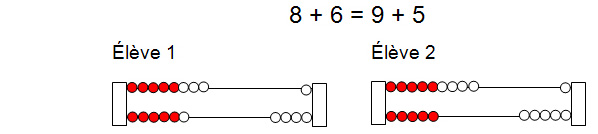
- L'enseignant met les élèves en contexte en leur racontant une partie pyjamas organisée pour 14 enfants. Quand vient le temps de se coucher, ils essaient tous de rester tranquilles dans un très grand lit superposé, mais, pendant la nuit, ils se mettent à passer de l'étage du haut à l'étage du bas parce qu'ils ont trop envie de bavarder avec différents amis. Au départ, il y a 8 enfants à l'étage du haut et 6 enfants à l'étage du bas.
- En groupe de deux, les élèves représentent ce problème simple à l'aide de bouliers compteurs.
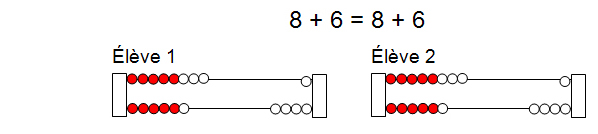
- Ensuite, l'enseignant réécrit le problème tout en modifiant 1 des termes de l'équation et en utilisant une case vide pour représenter le terme manquant qui permettrait de s'assurer que cet énoncé mathématique demeure vrai.
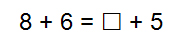
- Un des élèves déplace des boules sur son boulier afin de déterminer le nombre manquant.
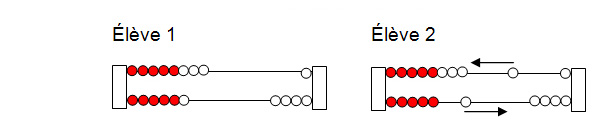
Remarque. – Les élèves peuvent recouvrir les boules inutilisées de leur boulier avec un chiffon s'ils ont du mal à fixer leur attention sur le côté du boulier qu'ils doivent « lire ».
Chaque élève écrit la nouvelle égalité numérique en se basant sur le nouvel arrangement représenté par leur boulier compteur.
- L'enseignant demande aux élèves de lui dire ce qui s'est passé à l'étage du bas (1 élève en est parti) et ce qui s'est passé à l'étage du haut (le même élève y est monté). L'enseignant pose ensuite cette question : « Est-ce qu'il y a toujours 14 élèves? ».
- L'élève 1 déplace ensuite des billes sur son propre boulier pour reproduire l'expression numérique de son coéquipier (9 + 5), et les deux équipiers les comptent tous les deux pour s'assurer que leurs bouliers sont identiques. Les élèves continuent de vérifier ce qui arrive à chacun des termes des additions lorsque des enfants se déplacent d'un étage à l'autre du lit superposé – soit 1 à la fois ou 2 à la fois (+ 1 et – 1 ou + 2 et – 2).
- Lors d'une discussion, l'enseignant guide les élèves afin de les amener à énoncer clairement cette stratégie de compensation, c'est-à-dire que l'on doit ajouter à un terme de l'addition ce que l'on a soustrait de l'autre (et vice versa) pour maintenir l'équilibre.
- L'enseignant oblige les élèves à pousser encore plus loin leur raisonnement en leur soumettant une série d'additions et en leur demandant de les résoudre mentalement. Par exemple :
5 + 5 = 5 + __ 5 + 5 = 6 + __ (Les élèves sont encouragés à utiliser la compensation au lieu de calculer mentalement.) 5 + 5 = 7 + __ (« Crois-tu que tu peux utiliser la même stratégie pour résoudre ce problème? ») 15 + 27 = 14 + __ (« Cette fois encore, utilise la même stratégie pour résoudre ce nouveau problème. ») 68 + 46 = __ + 45 (« Est-ce que la stratégie fonctionne toujours quand le nombre manquant change de place? »)
Remarque. – Quand les élèves doivent manipuler de plus grands nombres, il peut être utile de leur fournir des blocs de base dix pour les aider à développer des stratégies de compensation : ils peuvent alors déterminer plus facilement les nombres manquants en déplaçant des blocs d'une pile à une autre pour représenter des équations.