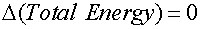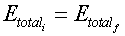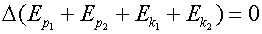Lesson 1 - Atwood's Pulley (massless pulley)
Atwood's Pulley (massless pulley)
simulates the motion of two masses connected by an ideal string passing over a massless pulley in order
to explore the concepts of mechanical energy, energy conservation, and energy transformation.
Prerequisites
Students should be
familiar with the concepts of
potential and kinetic energy.
Learning Outcomes
Students will become familiar with energy conservation and energy transformation.
Instructions
Students should understand the applet functions that are described in Help and ShowMe.
The applet should be open.
The step-by-step instructions in the following text are to be done in the applet.
You may need to toggle back and forth between instructions and applet if your screen space is limited.
Contents
- Calculating Potential Energy and Setting a Zero-point for Potential Energy
- Calculating Potential and Kinetic Energy
- Total Mechanical Energy of a System and Conservation of Energy
Please answer the following questions in the space provided.
1. Calculating Potential Energy and Setting a Zero-point for
Potential Energy
| In order to assign a numerical value to the potential energy of a
body, it is first necessary to define a "zero point" or reference
level at which the potential energy is considered to be 0 J. You
do this on the applet by repositioning the Ep Reference line by moving
it up or down. To see how this works, position the Ep Reference line to
be at the same height as the centre of the pulley as shown in the next
diagram.
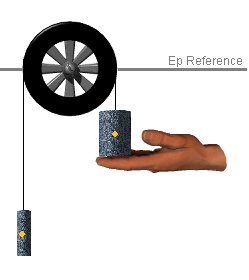
Set mass 1 to
equal 250 g and mass 2 to be 750 g.
- Are the initial potential energies for mass 1 and mass 2 positive,
negative, or zero in this case? Explain your answer.
- Run the applet (click
 ),
and produce a graph showing the potential energy for each mass as a
function of time. Explain why the graphs look the way they do. ),
and produce a graph showing the potential energy for each mass as a
function of time. Explain why the graphs look the way they do.
|
- Mass 1 climbs by 1.133 m and mass 2 drops by 1.133 m. Calculate
the change in potential energy for each mass. Recall that
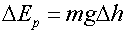 ,
where ΔEp is the change in potential
energy, m is the mass, g = acceleration of gravity and Δh
is the change in height. Show how the change in energy for each mass
can be measured from the graphs that you produced in question 2. ,
where ΔEp is the change in potential
energy, m is the mass, g = acceleration of gravity and Δh
is the change in height. Show how the change in energy for each mass
can be measured from the graphs that you produced in question 2.
- Its clear that we didn't pick the most convenient place for the Ep
Reference line. "Reset" the applet (
 ) and this time put the Ep Reference line through the yellow dot that
represents the centre of mass for mass 1. When released, mass 1 will
move above this line and its Ep will increase. Since mass 2 is already
above this line and it drops, its Ep will start at its maximum value
and then decrease. Calculate the initial potential energy for mass 2
relative to this new Ep Reference line and use the applet to verify
your calculation (hint: redo the graphs that you created in question
2). What is the initial potential energy for mass 2?
) and this time put the Ep Reference line through the yellow dot that
represents the centre of mass for mass 1. When released, mass 1 will
move above this line and its Ep will increase. Since mass 2 is already
above this line and it drops, its Ep will start at its maximum value
and then decrease. Calculate the initial potential energy for mass 2
relative to this new Ep Reference line and use the applet to verify
your calculation (hint: redo the graphs that you created in question
2). What is the initial potential energy for mass 2?
- Combine the initial potential energy for each mass (Ep1 + Ep2). This
represents the initial potential energy for the system. What is this
energy? Run the applet. What is the potential energy of the system now?
Are these two energies the same?
|
2. Calculating Potential and Kinetic Energy
|
In the previous example the initial potential energy of the system
was greater than the final potential energy (by about 5.56 J). What
happened to this energy?
Answer: When you click "Play", the masses begin
to accelerate. Mass 1 moves up, mass 2 moves down. A new energy form,
kinetic energy, is now being created. Recall, kinetic energy
is given by the expression 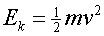 , where m is the mass and v is the velocity.
, where m is the mass and v is the velocity.
|
- Rerun the applet using the same mass values used in the previous section.
Produce kinetic energy-time graphs for each mass and a graph showing
velocity-time (the velocity will be the velocity for mass 2 - mass 1's
velocity is just the negative of this). Your graph should look something
like the one shown next.
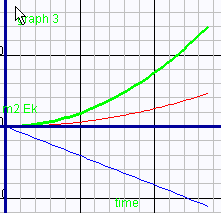
- How fast is each mass moving at t = 0.50 s? What is the kinetic
energy for each mass at this time? Answer this by calculating the kinetic
energy and then verify this result by inspecting the graph. (Tip: use
the "drag-and-zoom" control button to zoom-in on points of interest
on the graph. Alternately, generate a data table and look up the velocity
and energy at t = 0.50 s.)
- The total energy of the system is just the sum of all the kinetic
and potential energy terms at any instant. Find the total energy of
this system at t = 0.00 s, t = 0.50 s and t = 0.68 s.
What do you notice about these three numbesr?
|
3. Total Mechanical Energy of a System and Conservation of
Energy
The Atwood applet assumes that there is no loss of energy from the system.
This means that there is no frictional loss in the pulley and that air resistance
on the moving masses can be ignored. It is assumed that energy is conserved.
When this happens we can conclude that the total energy of the system is constant.
This can expressed in the following ways:
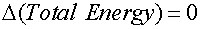 |
The net change in energy in the system is
zero. Energy is neither lost or created |
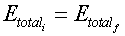 |
The total energy of the system before is equal to the total
energy of the system after any motion or change. |
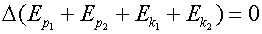 |
The individual expressions for the energy
can change but their sum must be zero. Increases in one term will be offset
by decreases in other terms. |
These are just three ways of stating the Principle of
Conservation of Mechanical Energy.
Set up the applet so that mass 1 = 200 g and mass 2 = 800 g. Please
fill out the following table and verify the results by using the Atwood applet:
| System |
Before Masses Released |
Masses Released and Mass One has Moved
Up 0.5 m |
| Ep1(J) |
|
|
| Ep2(J) |
|
|
| Ek1(J) |
|
|
| Ek2(J) |
|
|
| E total (J) |
|
|
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004

 ),
and produce a graph showing the potential energy for each mass as a
function of time. Explain why the graphs look the way they do.
),
and produce a graph showing the potential energy for each mass as a
function of time. Explain why the graphs look the way they do.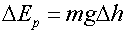 ,
where ΔEp is the change in potential
energy, m is the mass, g = acceleration of gravity and Δh
is the change in height. Show how the change in energy for each mass
can be measured from the graphs that you produced in question 2.
,
where ΔEp is the change in potential
energy, m is the mass, g = acceleration of gravity and Δh
is the change in height. Show how the change in energy for each mass
can be measured from the graphs that you produced in question 2. ) and this time put the Ep Reference line through the yellow dot that
represents the centre of mass for mass 1. When released, mass 1 will
move above this line and its Ep will increase. Since mass 2 is already
above this line and it drops, its Ep will start at its maximum value
and then decrease. Calculate the initial potential energy for mass 2
relative to this new Ep Reference line and use the applet to verify
your calculation (hint: redo the graphs that you created in question
2). What is the initial potential energy for mass 2?
) and this time put the Ep Reference line through the yellow dot that
represents the centre of mass for mass 1. When released, mass 1 will
move above this line and its Ep will increase. Since mass 2 is already
above this line and it drops, its Ep will start at its maximum value
and then decrease. Calculate the initial potential energy for mass 2
relative to this new Ep Reference line and use the applet to verify
your calculation (hint: redo the graphs that you created in question
2). What is the initial potential energy for mass 2?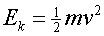 , where m is the mass and v is the velocity.
, where m is the mass and v is the velocity.