This document shows you how to use this applet in a step-by-step manner. You
should have the applet open; toggle back and forth between the ShowMe file and
the applet as you work through these instructions.
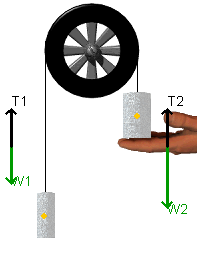
- A Free Body Diagram (FBD) for each mass can be produced by pressing
the Free Body Diagram control button. When you do this, the images
of the masses will fade slightly and force vectors representing the
weight and tension will appear (see the figure below). The
hand indicates that mass 2 is held before release. In this case, the
tension in the strings is entirely due to the weight of mass 1.
|
 |
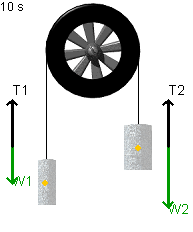
- Note that when you click "Play", the supporting
hand disappears and the masses move. The tensions shown in the strings
will change.
|
 |
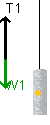
- The tensions in the supporting strings are not shown.
They can be easily calculated, however, by first finding the acceleration
for each mass and then applying Newton's second law . For example,
in the previous discussion of acceleration, we determined that mass
1 was accelerating upward at 3.92 m/s2. If we use the FBD
for mass 1 (shown on the left) and if we assign up as the positive
direction, the following force-equation is implied:
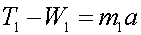
Since 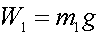 ,we find that ,we find that
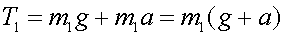
Since mass 1 = 0.300 kg and a = 3.92 m/s2, we find that
both T1 and T2 are equal to 4.12 N .
|
 |
- When you run the Atwood applet, you will see a horizontal line labeled
"Ep Reference". This line is used to define a position at
which the two masses have zero potential energy. You can capture this
line by positioning the mouse over it and then, holding down the left-mouse
button, drag up or down. When you "capture" the line, it will
fade slightly as shown below.
To illustrate this, adjust the masses so that mass 1 = 300 g and
mass 2 = 700 g.
|

EP Reference not yet "captured"
by the mouse |
EP Reference has been"captured" by the mouse
|
- Each mass has a yellow dot that indicates its centre of
mass. To see how to use the EP Reference line effectively, position
the EP Reference line so that it passes through the yellow dot (center
of mass) for mass 1.
|
 |
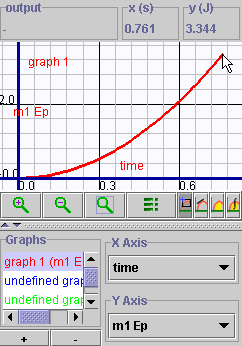
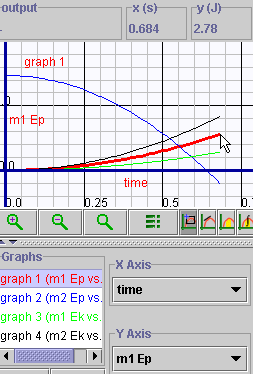
- Click "Play", wait until the motion stops, and
then click "View Graph". Produce a graph with time on the
x-axis and the potential energy of mass 1 (m1 EP) on the y-axis. You
should see a graph very similar to the one below. Note that the potential
energy for mass 1 starts at zero - just as we would expect, since we
put the EP Reference line at this point. Also note that when the motion
stopped, mass 1 had ascended to a point 1.133 m above the reference
line. Since
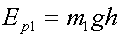 (where
Ep1 is the potential energy of mass 1 and h is the height
through which it moved), we can insert the numbers to find that: (where
Ep1 is the potential energy of mass 1 and h is the height
through which it moved), we can insert the numbers to find that:
Ep1 = (0.300 kg)(9.81 m/s2)(1.133
m) = 3.33 J .
You can verify this calculation by inspecting the graph below.
|
- A powerful feature of the grapher is the ability to create new variables
that are not listed in the original drop-down menu of variables to plot.
Since we plotted the potential and kinetic energy terms for the two
masses in the previous example, it is instructive to ask "What
would the sum of all of these terms look like?". To do this, close
the graph and click the data collection button (
 ).
A drop-down menu appears ( ).
A drop-down menu appears ( )
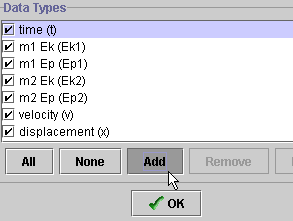
- choose "Select Data". A dialogue box like the one shown
below will appear. Since you want to create an expression that does
not appear in those listed, click "Add". )
- choose "Select Data". A dialogue box like the one shown
below will appear. Since you want to create an expression that does
not appear in those listed, click "Add".
|
 |
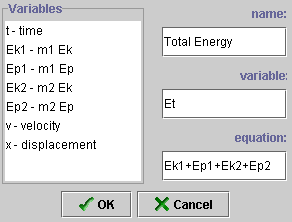
- After clicking "OK" (
 ),
a new dialogue box opens. Fill in the blank spaces exactly as shown
below. Be very careful to type the variables exactly as they appear
in the list of available variables. You only can build equations out
of the pre-existing set of variables. When you are finished, click "OK".
You now have created a variable called "Total Energy" and
it is available for plotting on the graph. ),
a new dialogue box opens. Fill in the blank spaces exactly as shown
below. Be very careful to type the variables exactly as they appear
in the list of available variables. You only can build equations out
of the pre-existing set of variables. When you are finished, click "OK".
You now have created a variable called "Total Energy" and
it is available for plotting on the graph.
|
 |
- To plot "Total Energy", you will need to add
one more equation to the graph. Press the small "+" button
at the bottom of the graph panel (as shown below). A new graph,
labeled "undefined graph" appears at the bottom of the previous
list of 4 graphs.
|
 |
- Proceed as you would with any other graph. Note that this
time when you click the "X axis" or "Y axis" buttons,
a new variable appears in the list - "Total Energy". Select
time for the x-axis and Total Energy for the y-axis.
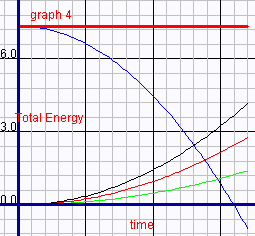
- Next, click "Reset" and then click "Play". This
will update the graph, and also use the newly defined variable Total
Energy. When finished, you should see a graph very similar to the one
below.
|
 |
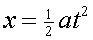 , and
that we can rearrange this equation to give us
, and
that we can rearrange this equation to give us 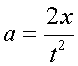 ,
then it is a straight-forward calculation to show that acceleration
a = 3.92 m/s2.
,
then it is a straight-forward calculation to show that acceleration
a = 3.92 m/s2.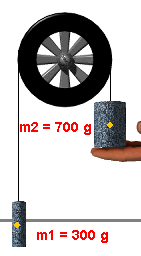
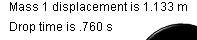


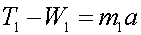
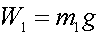 ,we find that
,we find that 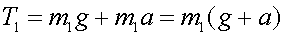




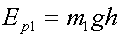 (where
Ep1 is the potential energy of mass 1 and h is the height
through which it moved), we can insert the numbers to find that:
(where
Ep1 is the potential energy of mass 1 and h is the height
through which it moved), we can insert the numbers to find that:

 ).
A drop-down menu appears (
).
A drop-down menu appears ( )
- choose "Select Data". A dialogue box like the one shown
below will appear. Since you want to create an expression that does
not appear in those listed, click "Add".
)
- choose "Select Data". A dialogue box like the one shown
below will appear. Since you want to create an expression that does
not appear in those listed, click "Add".
 ),
a new dialogue box opens. Fill in the blank spaces exactly as shown
below. Be very careful to type the variables exactly as they appear
in the list of available variables. You only can build equations out
of the pre-existing set of variables. When you are finished, click "OK".
You now have created a variable called "Total Energy" and
it is available for plotting on the graph.
),
a new dialogue box opens. Fill in the blank spaces exactly as shown
below. Be very careful to type the variables exactly as they appear
in the list of available variables. You only can build equations out
of the pre-existing set of variables. When you are finished, click "OK".
You now have created a variable called "Total Energy" and
it is available for plotting on the graph.


