ShowMe - Circular Motion: Horizontal
Circular Motion: Horizontal simulates the motion of a mass on a rigid rod
that is moving along a horizontally-oriented circular path. It also explores
the relationship between the inward force acting on an object travelling in
uniform circular motion and the object's mass, path radius, and speed.
This document shows you how to use this applet in a step-by-step manner.
You should have the applet open; toggle back and forth between the ShowMe file
and the applet as you work through these instructions.
Contents
- Using the Free Body Diagram to Illustrate Inward Force, Centripetal
Acceleration, and Tangential Velocity
- Adjusting the Basic Parameters: Mass, Radius, Velocity
- Demonstrating the Relationship between Inward Force, Centripetal
Acceleration, and the Basic Parameters
- Contrasting Circular and Tangential Motion
1. Using the Free Body Diagram to Illustrate Inward Force, Centripetal Acceleration,
and Tangential Velocity
- Give the mass a small velocity (5 m/s) by adjusting the velocity
control at the bottom of the applet, and then click "Play".
|
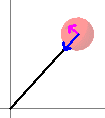
- Once the mass begins to move, click "FBD" to display
the free body diagram and tangential velocity vector.
Note that both vectors remain fixed in magnitude. The blue vector
represents the tension in the rod, which pulls the ball at right angles
to its direction of motion (magenta vector). This illustrates the
essential role that the inward force plays: the inward force accelerates
the mass by changing its direction of motion rather than the
magnitude of its velocity.
|
 |
- Try changing the velocity and note how the magnitudes
of the two vectors change in response to this.
|
2. Adjusting the Basic Parameters: Mass, Radius, Velocity
The basic parameters for this applet are easily adjusted by moving the appropriate
slider.
3. Demonstrating the Relationship between Inward Force, Centripetal Acceleration,
and the Basic Parameters
- The Circular Motion: Horizontal applet can be used to illustrate the
basic connection between force, velocity, and radius. Recall that the
expression for the inward or centripetal force is
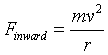 where m is the mass, v the velocity, and r the
radius.
where m is the mass, v the velocity, and r the
radius.
|
- As an example, set the mass to 2 kg, the radius to
5 m, and the velocity to 5 m/s. You should observe that the
output panel along the top of the applet displays both the inward force
and tension in the rod. Both are equal to 10 N.
|
- Since you know the magnitude of the inward force and the
mass being accelerated, you can also calculate the centripetal acceleration.
In the previous example it is easy to see that since F= ma,
a = 10 N/ 2 kg = 5 m/s2. This is also consistent with
the expression
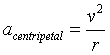 . .
|
4. Contrasting Circular and Tangential Motion
- The applet Circular Motion: Horizontal is particularly effective
at contrasting circular and tangential motion.
- To illustrate this, pick a convenient velocity - for example, 5 m/s
- and click "Play". Once the motion begins, use "Cut"
to break the connection between the rod and ball. Observe the abrupt
transition from circular motion to linear motion. Since there is no
longer a net force acting on the ball, it will (according to Newton's
First Law) continue to move at a constant velocity. This means that
neither the magnitude nor the direction of the velocity will change.
Note that the both the Tension and Inward force values drop to zero
in the output display panel.
|
Physics 20-30 v1.0
©2004 Alberta Learning (www.learnalberta.ca)
Last Updated: June 16, 2004

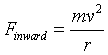 where m is the mass, v the velocity, and r the
radius.
where m is the mass, v the velocity, and r the
radius.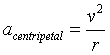 .
.