ShowMe - 1D Non-Uniform Motion Builder Graphing (pos, vel, acc)

1D Non-Uniform Motion Builder Graphing (pos, vel, acc) simulates the uniform motion of an object and constructs position-time and velocity-time graphs to analyze two-dimensional motion.

This document shows you how to use this applet in a step-by-step manner. You should have the applet open; toggle back and forth between the ShowMe file and the applet as you work through these instructions.

Contents

  1. How to Make a Motion Script
  2. How to Run a Motion Script and Graph Its Motion
  3. How to Edit a Motion Script

1. How to Make a Motion Script

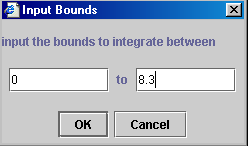
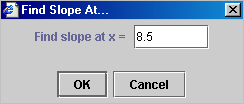
  1. A motion script is a set of instructions that you enter in the 1D Non-Uniform Motion Builder Graphing (pos, vel, acc) applet by clicking "Add" (image) and then filling out the information required in an information window that opens. A sample window is shown here. There are four pieces of information that you can alter:
    • Time (s): this is the amount of time for the motion in this script
    • TimeStep (s): Time step is the interval of time between successive calculations of the motion. If you are unsure about this then it is best to leave it at the default value of 0.01 s. Normally the time step should be about 1 percent of the entire time for the motion. For example, if you wanted the motion to occur over a span of 100 s, then the time step should be increased to be about 0.10 s. Too big a time step will result in a drop of precision in the simulation of the motion. Too small a time step will result in the generation of too much "data" when the applet does its calculations.
    • Velocity X (m/s): set this for whatever value is needed.
      (NOTE: do not put units with your values - they are already included as shown. )
    • Acceleration X (m/s^2): set the acceleration here.


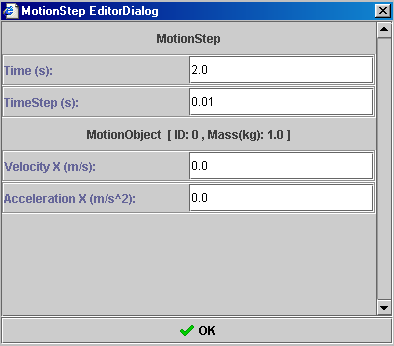
  2. Click "OK" (image) to close the menu and save the motion script.
image
  1. You can make as many scripts as you wish by simply clicking the "add script" button and supplying the required information. The figure shown on the right shows three scripts. The information for each script is shown. The total time required for the entire motion will just be the sum of the times for each script. In this example the total time will be 2.0 s + 3.0 s + 2.0 s = 7.0 s.
image
  1. As an example, create a motion that has the following three parts, each described by a script:
    1. A ball accelerates from rest at 3 m/s2 for 2 s.
    2. It coasts at a constant speed of 6 m/s for 5 seconds.
    3. The ball begins to decelerate at -1 m/s2 for 6 s.

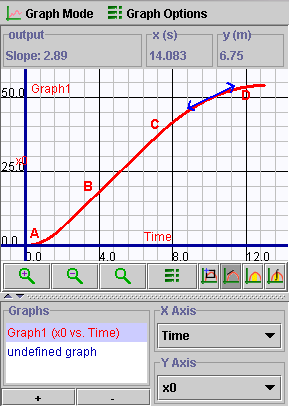
    Enter this information into MotionBuilder. When finished, your motion scripts should appear in the Motion Script Display Window and look like the following
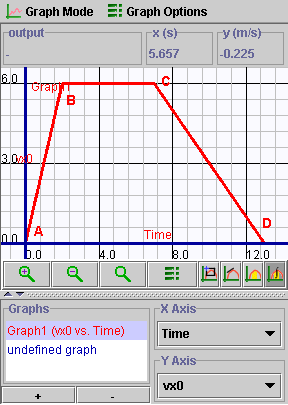
image

2. How to Run a Motion Script and Graph Its Motion

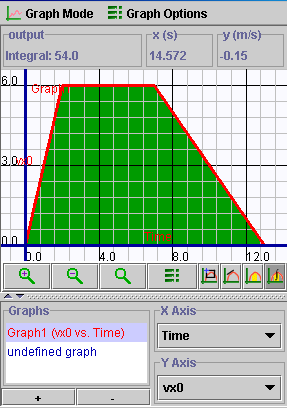
  1. You can run a motion at any time by clicking "Play" (image). If you are editing a motion script or in the motion script data entry window then you will need to close this first before you can run the motion. You can pause the motion by clicking "Pause" (image) and resume by again clicking "Play". To start over, click "Reset" (image ).
  2. One of the most important features of this applet is the grapher. You can view a graph of the motion by clicking "Graph" (image) . You may do this after the motion is complete or you can open the graph and have it visible as the motion unfolds.
  1. For example, the figure on the right shows the distance-time graph for the motion scripts that you created in the previous section. Define the X axis to be time and the Y axis to be the x-coordinate of the ball's location. This is listed as x0. You can now use the graphing tools to inspect the graph. (Note: the letter labels have been added.)
  2. Use the Slope tool (click image) to measure the slope of the graph at various locations along the graph. When you do this, a blue double-headed arrow will appear that will travel along the distance-time graph as you move the mouse along the graph. The slope of the graph is given in the output window. From this you can see:
    • In section A-B the motion is accelerated and the slope will increase from 0 to 6 m/s as you slide up the curve
    • In section B-C the motion is constant and the slope is constant at 6 m/s
    • In section C-D the motion is decelerating and the slope changes from 6 m/s to 0 m/s.
  3. Verify that at t = 8.5 s, the ball's velocity was 4.5 m/s.
image
(Grapher tips: double-click on the slope-tool button image, this will open the following input window that allows you to measure the slope at a specific point)
image
  1. Another useful graph that you can construct is a velocity-time graph. Again set the X-axis to be Time and choose the Y-axis to be vx0. Your graph should look similar to the one shown on the right. By inspection you see that:
    • AB represents script 1, time = 2 s, a = 3 m/s2
    • BC represents script 2, time = 5 s, v = 6 m/s and a = 0 m/s2
    • CD represents script 3, time = 6 s, a = -1 m/s2
image
  1. An important property of velocity-time graphs is the area between the graph and the time axis. Click "Area" (image) and position the mouse at t = 0 s. Hold down the left mouse button and drag across the graph to t = 13 s. As you do this, the area between the time axis and the graph is painted green and the output panel now reads Integral and gives a running value for the area that you are creating. If you paint all the way to t = 13 s you will see that the size of the green area is equal to 54.0 m. Note: the grapher will not supply units for this - you must recognize that the area must have units of (m/s) X (s) = m and put these in yourself! So the distance traveled in this motion is 54.0 m.
image
  1. As an example, use this feature to verify that after 8.3 s the ball will have traveled 43 m.
    (Grapher tip: another way to tell grapher what area to measure is to double-click on "Area" (image). This opens up an input bounds dialogue box similar to the one shown below. Put in the appropriate values for the range over which you wish to measure the area. In this case the values 0 and 8.3 where used.)
image

3. How to Edit a Motion Script

  1. To change a motion script or to add or delete scripts, use the controls in the upper part of the applet. For example, to modify an existing script, click on that script. The figure on the right shows the set of motion scripts that you created earlier and indicates that the second script is the one that you have selected.
  2. Click "Edit" (image). The Motion Editor Dialogue Window opens and you can now make any necessary changes.
image
  1. To add another script, click "Add" (image).
  2. To delete a script click "Remove" (image).
  3. To remove all scripts, click "Remove All" (image ).

Physics 20-30 v1.0back to top
©2004 Alberta Learning (www.learnalberta.ca)

Last Updated: June 16, 2004