Transformations

Strand: Shape and Space (Transformations)
Outcomes: 5, 6

Step 1: Identify Outcomes to Address

Guiding Questions

What do I want my students to learn?
What can my students currently understand and do?
What do I want my students to understand and be able to do, based on the Big Ideas and specific outcomes in the program of studies?

See Sequence of Outcomes from the Program of Studies

Strand: Shape and Space (Transformations)

Grade 3

Grade 4

Grade 5

Specific Outcomes
	There are no outcomes in Shape and Space (Transformations). Outcomes from Shape and Space (3-D Objects and 2-D Shapes) include:
6.	Describe 3-D objects according to the shape of the faces and the number of edges and vertices.
7.	Sort regular and irregular polygons, including: triangles quadrilaterals pentagons hexagons octagons according to the number of sides.

Specific Outcomes

Demonstrate an understanding of congruency, concretely and pictorially.

Demonstrate an understanding of line symmetry by:

identifying symmetrical 2-D shapes
creating symmetrical 2-D shapes
drawing one or more lines of symmetry in a 2-D shape.

Specific Outcomes
8.	Identify and describe a single transformation, including a translation, rotation and reflection of 2‑D shapes.

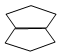
Big Ideas

Congruency and symmetry are geometric properties. These properties can be used to determine what makes some shapes alike and different.

Congruent 2-D shapes are "geometric figures that have the same size and shape" (Alberta Education 1990, p. 198). Symmetrical 2‑D shapes are geometric figures "that can be folded in half so that the two parts are congruent" (Alberta Education 1990, p. 205).

Symmetrical and congruent shapes are closely connected. Any symmetrical shape can be divided into two congruent parts along the line of symmetry; however, not every composite shape made up of congruent figures is symmetrical. For example,

	This regular hexagon is symmetrical. The line of symmetry shown in the diagram divides the hexagon into two congruent shapes, each shape is a pentagon. This composite shape is made up of two congruent pentagons. It is not symmetrical.
	This composite shape is made up of two congruent pentagons. It is symmetrical.

It is the relation of congruent shapes to one other in the composite shape that determines whether or not this composite shape is symmetrical.

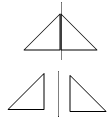
A shape remains the same size and shape when transformed using translations, reflections or rotations; i.e., the object and the image in these transformations are congruent. Symmetrical shapes form a subset of reflections. A reflection results in a symmetrical composite shape when the mirror line used to reflect a shape aligns with one side of the shape. For example:

This reflection results in a composite shape that is symmetrical.
The mirror line and the axis of symmetry coincide.

This reflection does not result in a composite shape but rather two separate shapes that are congruent. The mirror line is shown in the diagram but it is not the axis of symmetry.