 Grade 5
Grade 5
FractionsStep 1: Identify Outcomes to AddressGuiding Questions
Big IdeasStudents develop and demonstrate understanding of equivalent fractions and the comparison of fractions by connecting the concrete, pictorial and symbolic representations. They should be encouraged to use a variety of strategies to make sense out of fractions relating to parts of a whole region or whole set. For example, students can use pattern blocks, buttons, fraction strips, fraction circles or geoboards to concretely represent fractions and then draw appropriate diagrams together with the corresponding symbolic representations. By observing students, asking questions and listening to their explanations, the teacher probes for deeper understanding. The Professional Standards for School Mathematics states that it is beneficial for students to create their own models and allow for some confusion to reveal what students do and do not understand (NCTM 1991, p. 163). Van de Walle and Lovin (2006) expand upon this idea when they state that to help "students create an understanding of equivalent fractions is to have them use models to find different names for a fraction" (p. 81). Van de Walle and Lovin (2006) provide the following big idea about equivalent fractions:
Problem solving plays a major role in developing mathematical power with fractions. As students create and solve a wide variety of problems related to fractions, they must be engaged in "making conjectures and constructing arguments, validating solutions and evaluating the reasonableness of mathematical claims" (NCTM 1991, p. 21). Assessment of problem solving requires that the teacher "look beyond the answer to the reasoning behind the solution. This evidence can be found in written and oral explanations, drawings and models" (NCTM 2000, p. 187). As teachers reflect on this assessment data, they are able to plan future instruction that best suits the students' needs in developing understanding of fractions or any other mathematical concept. Van de Walle and Lovin (2006) elaborate further: "In a problem-based classroom, students can develop an understanding of equivalent fractions and also develop from that understanding a conceptually based algorithm" (p. 81). They go on to caution that an instructional error is to formulate the rule too quickly. It is important that students construct their own meaning and use intuitive methods first. Using visual images of fractions such as fractions strips should help many students to think flexibly in comparing fractions (NCTM 2000, p. 216). Principles and Standards for School Mathematics provides the following example to illustrate how a student might communicate with understanding that
The As students develop understanding of equivalent fractions, they are able to use them to compare fractions with different denominators. By finding common denominators, the fractions are then compared by looking at which numerator is greater; i.e., which fraction has more of the same-sized parts (Van de Walle and Lovin 2006, p. 76). |
|||||||||||||||||||||||||||||||||||||||||||||









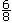 , if the eighths are taken in twos, then each pair of eighths is a fourth. The six-eighths then can be seen to be three-fourths" (p. 66).
, if the eighths are taken in twos, then each pair of eighths is a fourth. The six-eighths then can be seen to be three-fourths" (p. 66). 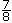
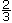 .
.