Independent Events
Strand: Statistics and Probability (Chance and Uncertainty)
Outcome: 2
Step 1: Identify Outcomes to Address
Guiding Questions
- What do I want my students to learn?
- What can my students currently understand and do?
- What do I want my students to understand and be able to do, based on the Big Ideas and specific outcomes in the program of studies?
 See Sequence of Outcomes from the Program of Studies
See Sequence of Outcomes from the Program of Studies
Big Ideas
- The probability of an event is a number between 0 (impossible) and 1 (certain). It is a measure of the chance that a given event will occur. A probability of
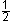 indicates an even chance of the event occurring.
indicates an even chance of the event occurring.
- Probability is a way to measure uncertainty. It involves predicting the likelihood of an event occurring over a period of time rather than predicting the likelihood of occurrence of an event for a specific time. For example, when rolling a die, we expect a two to occur about one sixth of the time when we conduct a large number of rolls; however, we cannot predict with much certainty what the next roll of the die will be.
- Theoretical probability of an event is the ratio of the number of outcomes in an event to the total number of possible outcomes, when all possible outcomes are equally likely.
- Experimental probability or relative frequency of an event is the ratio of the number of observed occurrences of the event to the total number of trials. The greater the number of trials, the closer the experimental probability approaches the theoretical probability.
- Two events are independent if the fact that one event occurs does not affect the probability of the second event occurring.
Adapted from John A. Van de Walle, LouAnn H. Lovin, Teaching Student-Centered Mathematics: Grades 5–8, 1e (pp. 333, 334). Published by Allyn and Bacon, Boston, MA. Copyright © 2006 by Pearson Education. Reprinted by permission of the publisher.
 Grade 8
Grade 8








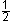 indicates an even chance of the event occurring.
indicates an even chance of the event occurring.