Creating Meaningful Activities
There is no other decision that teachers make that has a greater impact on students’ opportunity to learn and on their perceptions about what mathematics is than the selection or creation of the tasks with which the teacher engages the students in studying mathematics.
(Lappan and Briars 1995, p. 138)
Effective mathematics classrooms are ones in which students and teachers are engaged in dynamic mathematical activities that involve solving problems through logical reasoning, justifying procedures and solutions, employing multiple representations of concepts, and making connections between math and everyday life (Cohen and Ball 2001; Donovan and Bransford 2005; Hiebert 2005; Schielack et al. 2006; Stigler and Hiebert 1999).
When designing or selecting an activity or task, Romberg and Kaput (1999) suggest considering five questions:
- Does the task lead anywhere?
- Does the task lead to model building?
- Does the task lead to inquiry and justification?
- Does the task involve flexible use of technologies?
- Is the task relevant to students?
Adapted with permission from Thomas A. Romberg and James J. Kaput, "Mathematics Worth Teaching, Mathematics Worth Understanding," in Elizabeth Fennema and Thomas A. Romberg (eds.), Mathematics Classrooms that Promote Understanding (Mahwah, NJ: Lawrence Erlbaum Associates, 1999), pp. 9, 10, 11, 12.
When involved in learning activities, students must be given time to:
- construct relationships
- extend and apply mathematical knowledge
- explore how ideas are connected
- find alternate solutions
- justify their thinking
- extend the task or problem
- create generalizations
- reflect on the experience
- communicate what they have done and what they understand to others
- make the mathematical knowledge their own.
Effective activities should be embedded within lessons that are structured to build coherence and help students make connections that are not inherently obvious. Like a good story, the events should be organized and interconnected so that each one is logically connected to the others.
Providing Context for Activities
It is important to design or select worthwhile mathematical activities that are embedded within a meaningful context that both engages the learners and yields insights into important, worthwhile mathematics. The following are examples of how context can be provided for mathematical activities:
Personal Stories
Example:
The Grade 2 students arrived back at Red Deer Lake School after a snowy day and wanted to know how the school fan-out system worked. When did the principal get phoned in the morning? Who did he phone? How long did it take to phone every student in the school? Were there different ways to organize a fan-out system for a school? Which fan-out system took the least amount of time to reach all students?
Seizing the opportunity, the teacher turned students' questions and wonderings back to them. They spent the morning exploring various fan-out systems, inventing their own, debating the merits of each and deciding on the most effective and efficient fan-out system for a school.
Personal stories provide natural opportunities for connecting math to everyday life. Opportunities to turn students’ stories, questions and wonderings into a worthy, mathematical exploration await teachers who are attuned to the curriculum, the subject discipline and their students. Traditional and cultural personal stories can also provide a context for mathematical inquiry.
Literature
Example:
If the World Were a Village: A Book about the World's People by David J. Smith provides a wonderful opportunity for students to grasp various features of the world's population. By shrinking the world's population to a village of 100, students have the opportunity to understand better who we are, how we live and how fast we are growing. It provides an opening to explore various number concepts, such as fractions, decimal fractions, percent, proportion, scale and ratio, as they come to understand the world's people through number.
Many other published stories reflect mathematical principals and understandings; e.g.:
- Anno, Mitsumasa and Tsuyoshi Mori. Anno's Three Little Pigs. London, UK: The Bodley Head, 1986.
- Burns, Marilyn. The Greedy Triangle. New York, NY: Scholastic, 1994.
- Clement, Rod. Counting on Frank. Milwaukee, WI: G. Stevens Children's Books, 1991.
- Enzensberger, Hans Magnus. The Number Devil: A Mathematical Adventure.New York, NY: Henry Holt, 1998.
- Schwartz, David M. How Much Is a Million? New York, NY: Lothrop, Lee & Shepard Books, 1985.
- Scieszka, Jon and Lane Smith. Math Curse. New York, NY: Viking, 1995.
- Tahan, Malba. The Man Who Counted: A Collection of Mathematical Adventures. New York, NY: Norton, 1993.
Current Events
Examples:
- From the UN millennium goals, what would it take to reduce by half the proportion of people living on less than a dollar a day?
- How might you conduct a count of a species like the polar bear (or another animal that is always moving) to determine whether its population is decreasing?
- Is the quality of your local water improving? Collect evidence over time to determine whether this is the case.
Historical Accounts
Examples:
Queen Dido Uses Her Wits: Forced to leave her home in Italy, Queen Dido arrived in Northern Africa in an area that became known as Carthage or modern-day Tunisia. She needed to purchase some land for herself and her servants. She went to King Jambas and convinced him that all she needed was the amount of land she could enclose with a bull's hide. The land she enclosed became the city of Carthage. How is this possible?
Descartes' Fly: Folklore has it that one day as René Descartes lay in bed, he watched a fly crawl along the ceiling. As he lay there, a flash on analytic geometry struck him. He wondered whether he might be able to relay the position and the path of the fly to someone who wasn't there to watch the fly. This would require that he be able to determine the relation connecting the fly's distances from two adjacent walls. Descartes is the creator of the Cartesian plane and analytic geometry.
Penalty for Divulging 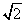 : Pythagoras was born around 560 B.C.E. He is known for forming a secret community of mathematicians. Pythagoras and his students believed that mathematics theories could be applied to anything, including nature, to predict and measure patterns or cycles. One day while on a ship, one of Pythagoras’s followers revealed to an outsider that : Pythagoras was born around 560 B.C.E. He is known for forming a secret community of mathematicians. Pythagoras and his students believed that mathematics theories could be applied to anything, including nature, to predict and measure patterns or cycles. One day while on a ship, one of Pythagoras’s followers revealed to an outsider that 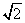 was not a rational number. As penalty, he was thrown overboard. was not a rational number. As penalty, he was thrown overboard.
Compelling Mathematical Truths
Examples:
- What do leaf arrangements, pine cones, sunflowers, daisies, drone bees and rabbits all have in common? Fibonacci numbers. An exploration into numbers and nature opens a rich mathematical terrain.
- Order and pattern have a particular soothing effect on humans. We are drawn to symmetry. From patterns in floor tiles and wall coverings to First Nations beadwork and butterfly wings, symmetry can be found almost everywhere. An inquiry into symmetry through decomposing figures into their congruent parts yields fascinating insight into symmetry.
For further information on designing or selecting worthwhile mathematical activities, see the Resource List. |





