Police :
Résultat(s) d’apprentissage :
  • 4e année, La forme et l’espace, n° 4
Matériel

Matériel

  • Un ensemble de figures
  • La fiche reproductible : « Patron des figures à découper » : les couleurs assignées à chacune des figures utilisées et le nombre requis de copies des pages de patrons pour environ 12 personnes sont indiqués dans le coin supérieur gauche de chacune de ces pages. Copiez les patrons sur du papier de couleur et plastifiez-les avant de découper les figures.
  • Un dé à 6 faces
  • Une copie de la fiche reproductible : « Les règles du jeu » pour chaque groupe de 2 à 4 élèves
Description : Dans cette activité, les élèves ont à reconnaître les figures qui doivent être combinées pour former les développements de divers objets à trois dimensions. Les élèves doivent visualiser les figures qui composent les développements. Ils peuvent manipuler les figures pour représenter les solides, mais l’activité est délibérément structurée pour que les élèves ne disposent que de très peu de temps de construction, l’intention première étant de favoriser la visualisation.

Activité

C’est une activité centrée sur le concept de développement qui fait appel à la visualisation de la part des participants.

  1. Présentez le jeu aux élèves. Expliquez-leur qu’à tour de rôle, ils doivent jeter le dé et prendre une figure dont le numéro correspond au nombre obtenu en jetant le dé. Chaque fois qu’un élève croira avoir constitué un ensemble de figures qui pourraient former le développement d’un objet à trois dimensions, il doit le démontrer au reste de son groupe et mettre cet ensemble de figures de côté. Expliquez aux élèves que seuls les ensembles de figures constitués de cette façon vaudront des points à la fin du jeu. Distribuez des copies des règles du jeu à tous les groupes. Dites aux élèves que, dans ce jeu, ils ne sont pas autorisés à combiner deux carrés pour former un rectangle ou deux rectangles pour former un carré.
  2. Allouez aux élèves un temps déterminé (15 minutes, par exemple) pour jouer. Au bout de ce temps, accordez encore un court moment aux groupes dont les membres n’ont pas tous joué le même nombre de tours.
  3. Demandez aux participants d’identifier et de nommer certains des objets dont ils ont fait les développements. Si vous disposez d’un rétroprojecteur, il pourrait être très efficace d’inviter les élèves à l’utiliser pour présenter leurs développements et les expliquer. Les termes conventionnellement admis pour désigner des formes, tels que prisme et pyramide, pourraient faire partie des objets de discussion.

    Bien que le jeu comporte un système de points, il peut être tout aussi efficace d’en faire uniquement une activité de coopération. Par exemple, cela peut très bien  fonctionner si les élèves travaillent deux par deux. Ils peuvent alors parler ensemble des objets qu’ils pourraient représenter et de la façon dont ils pourraient travailler, tout en faisant des observations telles que « Nous pourrions construire un tétraèdre avec les deux gros triangles et deux longs triangles, mais si on obtenait un 2 en jetant le dé, nous serions capables de construire une pyramide à base rectangulaire à la place. »

    Pendant ce jeu, il arrive que certains participants souhaitent avoir du matériel de manipulation tel que de la pâte à modeler ou de la plasticine pour pouvoir construire leurs objets à trois dimensions, tout en jouant. Cependant, cette activité vise à encourager les élèves à visualiser les combinaisons de figures convenables pour construire des objets à trois dimensions plutôt qu’à simplement essayer d’en construire concrètement. C’est pourquoi on n’utilise pas des figures conçues pour être fixées ensemble, ni aucune méthode pour les fixer de quelque façon.

  4. Renforcez l’apprentissage des élèves en leur demandant d’expliquer ce qu’ils ont appris sur la construction de types particuliers d’objets à trois dimensions. Par exemple, demandez-leur « De quelles figures auriez-vous besoin pour construire une pyramide à base carrée? De quelles figures aurais-je besoin pour construire un prisme à base carrée? Quelle est la différence entre une pyramide et un prisme? »

Éléments d’évaluation suggérés

Pendant ces activités, vous avez de nombreuses occasions d’observer et de noter le langage de vos élèves ainsi que les types d’objets qu’ils tentent de représenter. Vérifiez s’ils ont besoin de fabriquer concrètement un objet pour le voir ou si son développement leur suffit pour le visualiser. Doivent-ils d’abord le construire pour vérifier si ça fonctionne à tout coup ou sont-ils capables de visualiser cet objet?

Soyez attentif au langage qu’ils emploient pendant cette activité. Désignent-ils correctement les objets à trois dimensions par les noms appropriés?

À l’étape du renforcement, notez si les élèves peuvent désigner par leurs noms les figures requises pour construire des objets donnés et le vocabulaire qu’ils emploient pour les décrire.

Informations pour l’enseignant

Les objets qui peuvent être représentés sont tous des polyèdres. Il peut s’agir d’objets réguliers incluant des tétraèdres, des cubes, des octaèdres, et même des icosaèdres, mais plusieurs objets non réguliers peuvent aussi être utilisés. Certains des objets que les élèves devraient prendre un bout de temps à visualiser incluent des pyramides dissymétriques, dont deux exemples de développements apparaissent ci-dessous (la base étant au milieu).

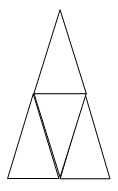Pyramide à base rectangulaire (ou pentaèdre) dissymétrique Pyramide à base triangulaire (ou tétraèdre) dissymétrique
Pyramide à base
rectangulaire (ou pentaèdre)
dissymétrique		 Pyramide à base
triangulaire (ou tétraèdre)
dissymétrique.

Source : Cartable Enseignement des concepts de forme et d’espace, 4e-6e année, Alberta Education, 2007.