Activité
- Distribuez des balances à plateaux, un sac en papier brun et des blocs-formes aux équipes d’élèves. Invitez les élèves à tester l’égalité d’une équation et à faire le lien entre l’équation et la balance en écrivant quelques équations d’égalité telles que 8 = 8. Invitez les élèves à discuter de la signification du signe d’égalité dans l’équation et sur la balance.
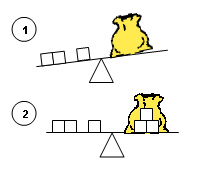
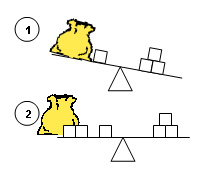
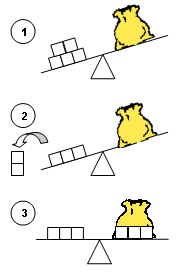
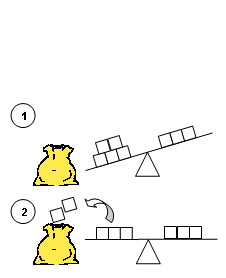
- Montrez aux élèves comment modéliser les situations reliées suivantes à l’aide de la balance et du sac en papier. Assurez-vous de leur présenter des exemples dont les sommes devraient apparaître tant du côté gauche que du côté droit du symbole d’égalité.
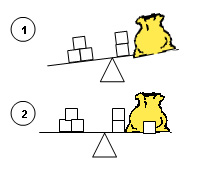
- Montrez aux élèves comment modéliser les situations indépendantes suivantes à l’aide de la balance et du sac en papier. Assurez-vous de leur présenter des exemples dont les sommes devraient apparaître tant du côté gauche que du côté droit du symbole d’égalité.
- Distribuez la feuille reproductible équations. Tous ensemble, les élèves de la classe essaient de déterminer comment chacune des situations illustrées pourrait être représentée sous la forme d’une équation, l’inconnue devant être représentée par un carré vide, un triangle vide ou un cercle vide.
- Installés deux par deux, invitez les élèves à modéliser de nouveaux problèmes reliés ou indépendants en utilisant dans chaque cas les 3 mêmes nombres. Ils écrivent également des équations pour représenter ces situations. Ils tracent dans chaque cas un carré, un triangle ou un cercle pour représenter l’inconnue.
- Invitez ensuite les équipes à échanger des problèmes avec une autre équipe. À l’aide de leur balance, les élèves de chaque équipe résolvent les problèmes qui leur ont été soumis sous la forme d’énoncés verbaux.
- De nouveau rassemblée, la classe entière discute des relations que chaque équipe est arrivée à établir entre les problèmes variés qui lui ont été soumis. Par exemple, après avoir résolu l’équation équivalente à 25 + 12 = 37, certains élèves diront qu’ils sont maintenant en mesure de résoudre l’équation équivalente à 25 + 12 = 37.
 |
 |
 |
| Reliées-résultat inconnu 2 + 1 = ? |
Reliées-changement inconnu 3 = 2 + ? |
Reliées-point de départ inconnu ? + 1 = 3 |
 |
 |
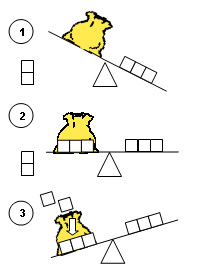 |
| Indépendantes-résultat inconnu 5 - 2 = ? |
Indépendantes-changement inconnu 5 - ? + 3 |
Indépendante-point de départ inconnu ? - 2 = 3 |
Informations pour l’enseignant
Dans cette tâche, les élèves sont appelés à s’interroger sur la signification des opérations d’addition et de soustraction, lesquelles sont souvent sous-jacentes, dans la formulation d’énoncés verbaux de problèmes.
L’enseignant guide ses élèves afin de les aider à prendre conscience du fait que même si les symboles utilisés pour représenter l’inconnue d’une équation donnée peuvent être différents (comme dans 15 + ▢ = 43 et 15 + △ = 43), cela n’a aucune influence sur la valeur de la solution. Les élèves devraient comprendre le plus tôt possible qu’il s’agit là de l’une des règles que les mathématiciens voués à l’étude des variables ont depuis longtemps adoptées d’un commun accord.
Types de problèmes
|
Résultat |
Changement inconnu |
Point de départ inconnu |
Problèmes |
Marion avait 15 billes, puis Juan lui en a donné 28 de plus. Combien de billes Marion a-t-elle en tout, maintenant? |
Marion a 15 billes. Combien de billes de plus faudrait-il lui donner pour qu’elle en ait 43 en tout? |
Marion avait quelques billes, puis Juan lui en a donné 15 de plus. Maintenant, Marion a 43 billes en tout. Combien de billes Marion avait-elle au départ? |
Problèmes indépendants |
Marion avait 43 billes, puis elle en a donné 15 à Juan. Combien de billes reste-t-il à Marion maintenant? |
Marion avait 43 billes, puis elle en a donné quelques-unes à Juan. Maintenant, il reste 15 billes à Marion. Combien de billes |
Marion avait quelques billes, puis elle en a donné 14 à Juan. Maintenant, il reste 28 billes à Marion. Combien de billes Marion avait-elle au départ? |
En 4e année, les élèves continuent leur apprentissage des variables en résolvant des additions et des soustractions. Toutefois, les problèmes qui leur sont soumis deviennent progressivement plus « statiques », c’est-à-dire de plus en plus difficilement assimilables à des actions ou des évènements, que ces derniers soient contextuellement reliés ou disjoints. Les élèves de 4e année aborderont des problèmes impliquant des relations du type partie-partie-tout et du type égalisation/comparaison.
Relation |
Tout inconnu |
Partie inconnue |
|||
Égalisation |
|
||||
Remarque – Vous trouverez à l’adresse suivante un applet en anglais qui permet aux élèves de s’exercer à l’équilibrage d’une balance : <http://teams.lacoe.edu/documentation/classrooms/linda/algebra/activities/balance/balance.html>.
Source : Patterns and Pre-Algebra, Gr. 4-6, Alberta Education, 2007. Activité traduite du cartable publié en anglais.








