Police :
Résultat(s) d’apprentissage :
  • 7e année, Les régularités et les relations, n° 6
Matériel

Matériel

  • 3 contenants de plastique transparent
  • un grand bassin (assez grand pour contenir la totalité des contenus qui seront versés dans les trois autres contenants)
  • ruban adhésif pour marquer des niveaux sur les contenants et les étiqueter
  • une chaudière d’eau (du riz ou du sable pourraient également convenir)
  • ustensile pour verser de l’eau (tasse, louche ou petit bocal)
  • Fiche reproductible : « Expressions » (facultatif)
Description : Les élèves transvident des contenants de mesures algébriques dans un bassin. Chemin faisant, ils explorent les expressions algébriques et les distinguent des équations algébriques.

Activité

  1. Démonstration devant la classe : Marquez aléatoirement un niveau sur chacun des contenants et utilisez les lettres p, q, et r pour étiqueter ces contenants.
  2. Demandez à un élève de remplir le contenant p et le contenant r jusqu’aux niveaux marqués sur chacun, puis de verser leur contenu dans le bassin. Écrivez p + r au tableau et expliquez aux élèves qu’il s’agit d’une façon de noter ce qui vient de se produire.
  3. Videz le bassin en reversant son contenu dans la chaudière, puis invitez un autre élève à venir en avant et à suivre cette directive : « Verse 2p et 3r dans le bassin. »
  4. Posez ces questions à la classe; Quelle(s) expression(s) pourrait/pourraient représenter ce qui s’est passé cette fois? De quelle façon pourriez-vous noter cette suite d’actions?

    5. Réponses possibles

    p + p + r + r + r       ou       2p + 3r

  5. Discussion : Qu’est-ce qui vous permet de dire que ces deux expressions décrivent ce qui s’est produit?
  6. Videz les contenants.  Invitez deux élèves à venir en avant pour faire la prochaine démonstration. Chuchotez-leur les directives suivantes : « Versez 4p dans le bassin, puis retirez-en un r. » Donnez quelques secondes aux deux élèves pour s’entendre. Demandez à la classe de regarder ce qui se passe et de noter l’expression qui pourrait représenter ces actions.
  7. Posez ces questions à la classe : Quelle(s) expression(s) pourrait/pourraient représenter ce qui s’est passé cette fois? De quelle façon pourriez-vous noter cette suite d’actions?

    8. Réponses possibles

    p + p + p + p – r     ou      4p – r

  8. Discussion : Qu’est-ce qui vous permet de dire que ces deux expressions décrivent ce qui s’est produit?
  9. Continuez d’inviter des couples d’élèves à venir faire des démonstrations et à discuter avec la classe des façons possibles d’écrire des expressions pour représenter leurs actions. Par exemple : « Versez 5r dans le bassin, puis retirez-en 2p. »
  10. Demandez aux élèves : Quelle(s) expression(s) pourrait/pourraient représenter ce qui s’est passé cette fois? De quelle façon pourriez-vous noter cette suite d’actions?

    11. Réponses possibles

    r + r + r + r + r – p – p     ou      (5r – 2p)

  11. Discussion : Qu’est-ce qui vous permet de dire que ces deux expressions décrivent ce qui s’est produit?
  12. Pour varier, vous pourriez donner par écrit leurs directives aux couples d’élèves que vous invitez à faire des démonstrations. Ainsi, le reste de la classe ne les entendrait pas, et cela pourrait les inciter à une écoute plus attentive.

    13. Exemple de directives :
    Versez trois r et trois q dans le bassin, puis retirez-en deux p.

  13. Posez ces questions à la classe : Quelle(s) expression(s) pourraient représenter ce qui s’est passé cette fois? De quelle façon pourriez-vous noter cette suite d’actions?

    14. Réponses possibles

    3r + 3q – 2p         3 (r + q) – 2p          r + r + r + q + q + q – p – p

  14. Discussion : Qu’est-ce qui vous permet de dire que ces trois expressions décrivent ce qui s’est produit?
  15. Et voici le défi final : Que devriez-vous faire pour que vos actions puissent se décrire comme ceci?

    16. 3(r + q) – 2p

  16. Invitez les élèves à partager leurs solutions et à en discuter.

Extension

  1. Invitez les élèves à formuler leurs propres expressions et à les tester.
  2. Invitez les élèves à travailler seuls ou en groupes pour rédiger les directives appropriées pour répondre aux questions suivantes :
    • Comment pourriez-vous démontrer que 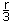r/3 (r/3, r ÷ 3) en utilisant le même matériel?
    • Et que feriez-vous pour démontrer que 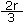 2r/3 (2r/3, 2r ÷ 3)?

Informations pour l’enseignant

Bien que les expressions ne peuvent pas toutes être associées à des évènements concrets, les élèves devraient construire des représentations mentales pour attribuer un sens aux relations qui existent entre les nombres et les symboles d’opérations dans les expressions, et cela avant qu’ils ne puissent les manipuler abstraitement.

Cette activité permet aux élèves de s’intéresser à certaines des notations conventionnelles qui sont utilisées pour formuler des expressions. Par exemple, pourquoi l’expression p + p + p peut-elle être réduite à 3p? Mais alors, pourquoi l’expression ne peut-elle pas être réduite à p + 3?

Source : Teaching Algebra Concepts, Gr. 7-9, Alberta Education, 2005. Activité traduite du cartable publié en anglais.