One-step Equations
Strand: Patterns and Relations (Variables and Equations)
Outcomes: 2, 3
Step 1: Identify Outcomes to Address
Guiding Questions
- What do I want my students to learn?
- What can my students currently understand and do?
- What do I want my students to understand and be able to do, based on the Big Ideas and specific outcomes in the program of studies?
 See Sequence of Outcomes from the Program of Studies
See Sequence of Outcomes from the Program of Studies
Big Ideas
Mathematics is often referred to as the science of patterns. Patterns permeate every mathematical concept and are found in everyday contexts. The various representations of patterns, including symbols and variables, provide valuable tools in making generalizations of mathematical relationships. Some characteristics of patterns include:
- There are different types of patterns that can be modelled in a variety of ways.
- Patterns using concrete and pictorial representations of a problem can be translated into patterns using numbers and symbols or letters in equations.
- Patterns are used to generalize relationships; e.g., numbers may be added or multiplied in any order without changing the sum or product.
- Equality is used to express relationships. The symbols used on either side of the equals sign represent a quantity. The equals sign is "a symbol of equivalence and balance" (NCTM 2000, p. 39).
- Patterns using symbols and variables provide a means of describing change mathematically; e.g., five more than, three less than.
- Variables and equations are used to mathematically model everyday problems that describe quantitative relationships.
Letter variables and symbols stand for any one of a set of numbers or objects and have multiple meanings. They are used as:
- representations of specific unknown values; e.g., 3 +
 = 15, 3 + n = 15
= 15, 3 + n = 15
- representations of quantities that vary or change; e.g.,
 +
+  = 15, x + y = 15
= 15, x + y = 15
- placeholders in a generalized expression or formula; e.g., c = 100 m, where c represents the number of centimetres and m represents the number of metres.
Adapted from John A. Van de Walle, LouAnn H. Lovin, Teaching Student-Centered Mathematics: Grades 3–5, 1e (pp. 290, 307). Published by Allyn and Bacon, Boston, MA. Copyright © 2006 by Pearson Education. Adapted by permission of the publisher.
Mathematician's rules or conventions dictate the use of variables for quantities that change or are dynamic.
- If the same variable or symbol is used repeatedly in the same equation, then there is only one possible solution for that variable or symbol; e.g., n + n = 20; the unique solution is n = 10.
- If different variables or symbols are used in the same equation, then there are many different possible solutions, one of which may be the same number replacing each variable or symbol; e.g., x + y = 20, other solutions include 0 + 20, 10 + 10,
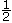 + 19
+ 19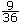 , and 25 – 5.
, and 25 – 5.
The majority of the work done by young students in using variables and symbols is focused on specific unknowns. They "use symbolic representations and drawings to help them solve problems and communicate their ideas" (Van de Walle and Lovin 2006, p. 303).
Algebraic reasoning is directly related to patterns because this reasoning focuses on making generalizations based on mathematical experiences and recording these generalizations using symbols or variables (Van de Walle and Lovin 2006).
 Grade 5
Grade 5








 = 15, 3 + n = 15
= 15, 3 + n = 15 = 15, x + y = 15
= 15, x + y = 15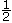 + 19
+ 19 , and 25 – 5.
, and 25 – 5.