Working with Decimal Numbers

Strand: Number
Outcomes: 8, 9, 10, 11

Step 1: Identify Outcomes to Address

Guiding Questions

What do I want my students to learn?
What can my students currently understand and do?
What do I want my students to understand and be able to do, based on the Big Ideas and specific outcomes in the program of studies?

See Sequence of Outcomes from the Program of Studies

Strand: Number

Grade 4

Grade 5

Grade 6

Specific Outcomes
9.	Represent and describe decimals (tenths and hundredths), concretely, pictorially and symbolically.
10.	Relate decimals to fractions and fractions to decimals (to hundredths).
11.	Demonstrate an understanding of addition and subtraction of decimals (limited to hundredths) by: using personal strategies to determine sums and differences estimating sums and differences using mental mathematics strategies to solve problems.

Specific Outcomes
8.	Describe and represent decimals (tenths, hundredths, thousandths), concretely, pictorially and symbolically.
9.	Relate decimals to fractions and fractions to decimals (to thousandths).
10.	Compare and order decimals (to thousandths) by using: benchmarks place value equivalent decimals.
11.	Demonstrate an understanding of addition and subtraction of decimals (limited to thousandths).

Specific Outcomes
2.	Solve problems involving whole numbers and decimal numbers.
8.	Demonstrate an understanding of multiplication and division of decimals (1-digit whole number multipliers and 1-digit natural number divisors).

Big Ideas

Conceptual understanding of decimals requires that the students connect decimals to whole numbers and to fractions. Decimals are shown as an extension of the whole number system by introducing a new place value, the tenths place, to the right of the ones place, separated by the decimal point. The tenths place follows the pattern of the base ten number system by iterating one tenth ten times to make one whole or a unit (Wheatley and Abshire 2002, p. 152). Similarly, the hundredths place to the right of the tenths place iterates one hundredth ten times to make one-tenth. Following this pattern, the thousandths place to the right of the hundredths place iterates one thousandth ten times to make one hundredth. Van de Walle and Lovin (2006) suggest that the concepts of whole number place value be reviewed prior to considering decimal numerals with students and they state:

"The base-ten place-value system extends infinitely in two directions: to tiny values as well as to large values. Between any two place values, the ten-to-one ratio remains the same. The decimal point is a convention that has been developed to indicate the units position. The position to the left of the decimal point is the unit that is being counted as singles or ones" (p. 107).

If a decimal numeral represents a quantity or a measure less than 1 unit, then a zero must be placed in the ones place to identify that there are no complete units in this numeral; e.g., one thousandth is written as 0.001 and is read as "one thousandth."

The connection between decimals and fractions is developed conceptually when students read decimals as fractions and represent them using the same visuals. For example, 0.8 is read as eight tenths and can be represented using fraction strips or decimal strips (Wheatley and Abshire 2002). Similarly, 0.008 is read as eight thousandths and can be represented using a thousandth square. Van de Walle and Lovin (2006) state, "Decimal numbers are simply another way of writing fractions" (p. 107).

As students use the same concrete representations for fractions and decimals and connect them to the same pictorial representations, they understand the connections between these two ways to represent part of a whole. The difference between fractions and decimals is in the symbolic representation where a fraction has a numerator and denominator while a decimal has a decimal point and place value (an extension of the whole numbers).

Various strategies are used in comparing and ordering decimals, including benchmarks, place value and equivalent decimals. Decimals could be sorted initially as being greater than, less than or equal to a benchmark such as 0.5. To facilitate the sorting process, the decimals should be all written with the same number of digits after the decimal; i.e., using equivalent decimals where necessary. For example, 0.52 is equivalent to 0.520. Conceptual understanding of equivalent decimals is based on connecting equivalent fractions to equivalent decimals. Therefore, 0.52 = .

An efficient and accurate way to order decimals is to use place value, as is done in ordering whole numbers. By building on students' prior knowledge about ordering whole numbers using place value and place value charts, the ordering of decimals is seen as continuing a pattern rather than something entirely new.

Estimation is crucial in the addition and subtraction of decimals. In fact, "students should become adept at estimating decimal computations well before they learn to compute with pencil and paper" (Van de Walle and Lovin 2006, p. 124). Through estimation, the students use number sense to determine if the answer is reasonable. By building on students' understanding of addition and subtraction of whole numbers, the pattern of place value is extended to decimals and the importance of adding the same place values continues; i.e., adding tenths to tenth, hundredths to hundredths and so on. Van de Walle and Lovin (2006) state,

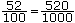Addition and subtraction with decimals are based on the fundamental concept of adding and subtracting the numbers in like position values—a simple extension from whole numbers (p. 107).