Working with Decimal Numbers
Strand: Number
Outcomes: 8, 9, 10, 11
Step 2: Determine Evidence of Student Learning
Guiding Questions
- What evidence will I look for to know that learning has occurred?
- What should students demonstrate to show their understanding of the mathematical concepts, skills and Big Ideas?
Using Achievement Indicators
As you begin planning lessons and learning activities, keep in mind ongoing ways to monitor and assess student learning. One starting point for this planning is to consider the achievement indicators listed in the Mathematics Kindergarten to Grade 9 Program of Studies with Achievement Indicators. You may also generate your own indicators and use them to guide your observation of the students.
The following indicators may be used to determine whether or not students have met this specific outcome. Can students:
- write a decimal for a given concrete or pictorial representation of part of a set , part of a region or part of a unit of measure?
- represent a given decimal using concrete materials or a pictorial representation?
- represent an equivalent tenth, hundredth or thousandth for a given decimal, using a grid?
- express a given tenth as an equivalent hundredth and thousandth?
- express a given hundredth as an equivalent thousandth?
- describe the value of each digit in a given decimal?
- write a given decimal in fraction form?
- write a given fraction with a denominator of 10, 100 or 1000 as a decimal?
- express a given pictorial or concrete representation as a fraction or decimal; e.g., 250 shaded squares on a thousandth grid can be expressed as 0.250 or
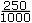 ?
?
- order a given set of decimals by placing them on a number line that contains the benchmarks 0.0, 0.5 and 1.0?
- order a given set of decimals including only tenths using place value?
- order a given set of decimals including only hundredths using place value?
- order a given set of decimals including only thousandths using place value?
- explain what is the same and what is different about 0.2, 0.20 and 0.2000?
- order a given set of decimals, including tenths, hundredths and thousandths, using equivalent decimals; e.g., 0.92, 0.7, 0.9, 0.876, 0.925 in order is 0.700, 0.876, 0.900, 0.920, 0.925?
- place the decimal point in a sum or difference using front-end estimation; e.g.,
for 6.3 + 0.25 + 306.158, think 6 + 306, so the sum is greater than 312?
- correct errors of decimal point placements in sums and differences without using paper and pencil?
- explain why keeping track of place value positions is important when adding and subtracting decimals?
- predict sums and differences of decimals using estimation strategies?
- solve a given problem that involves addition and subtraction of decimals, limited to thousandths?
Sample behaviours to look for related to these indicators are suggested for some of the activities found in Step 3, Section C, Choosing Learning Activities.
 Grade 5
Grade 5






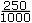 ?
?
