Improper Fractions and Mixed Numbers
Strand: Number
Outcome: 4
Step 5: Follow-up on Assessment
Guiding Questions
- What conclusions can be made from assessment information?
- How effective have instructional approaches been?
- What are the next steps in instruction?
A. Addressing Gaps in Learning
Students who have difficulty solving the basic facts using strategies will enjoy more success if one-on-one time is provided in which there is open communication to diagnose where the learning difficulties lie. Assessment by observing a student solving problems will provide valuable data to guide further instruction. Success in problem solving depends on a positive climate in which the students are confident in taking risks. By building on the existing understandings of each student and accommodating the individual learning styles, success will follow.
If the difficulty lies in solving the basic facts using strategies, use the following strategies:
- Draw on the prior knowledge of students, spending time reviewing proper fractions as part of a region and part of a set. Review the meaning of fractions and how they relate to a part and to a whole. Also, review the meaning of fractions as the division of numbers.
- Emphasize the similarities and differences between part of a region and part of a set.
- Provide everyday problem-solving contexts that students can relate to.
- Use a variety of concrete materials, such as folding paper, fraction strips, fraction circles, pattern blocks and geoboards. Connect the concrete to diagrams and symbols as students develop understanding of improper fractions and mixed numbers.
- Allow students to use concrete materials, as long as necessary, to establish an understanding of the concepts.
- Emphasize the similarities and differences between improper fractions and mixed numbers.
- Prior to ordering mixed numbers and improper fractions, review ordering proper fractions using benchmarks (Grade 4, Number, Outcome 8) and equivalent fractions (Grade 5, Number, Outcome 7). Encourage flexibility in choosing strategies to order fractions.
- Connect the number line to concrete fraction strips, recognizing that the number line is very abstract for many students.
- Encourage students to skip count on the number line to locate the position of various fractions; e.g., to find
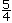 on the number line, skip count by quarters. Remind students that the numerator counts and the denominator tells what is being counted.
on the number line, skip count by quarters. Remind students that the numerator counts and the denominator tells what is being counted.
- Ask guiding questions to direct student thinking. See the examples provided in Step 4, Part B: One-on-one Assessment.
- Provide time for students to explore and construct their own meaning rather than being told.
- Encourage flexibility in thinking as students describe various ways to connect mixed numbers with improper fractions and to order fractions.
- Have students share their thinking with others so that students, who are having some difficulty, hear (in 'kid' language) how another person thinks about improper fractions and mixed numbers.
B. Reinforcing and Extending Learning
Strategies for Reinforcing and Extending Learning 
 Grade 6
Grade 6






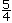 on the number line, skip count by quarters. Remind students that the numerator counts and the denominator tells what is being counted.
on the number line, skip count by quarters. Remind students that the numerator counts and the denominator tells what is being counted.

