Activité
- Présentez les carreaux algébriques pour représenter des nombres entiers positifs et négatifs :
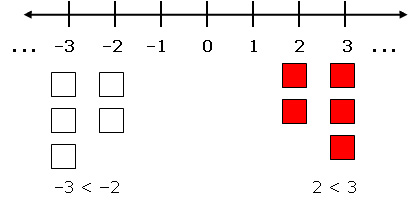
- Comparez les entiers relatifs à l’aide de carreaux algébriques :
- Présentez les entiers opposés à l’aide d’un exemple tiré de la vie courante : Tu gagnes 1 $ et tu dépenses 1 $. Combien d’argent te reste-t-il?
- Présentez aux élèves les sommes nulles.
- Faites l’exercice Valeur zéro avec les élèves.
- Guidez les élèves à faire une addition d’entiers relatifs en leur proposant le problème suivant : Tu gagnes 2 $, puis tu dépenses 5 $. Combien d’argent te reste-t-il? Nous pouvons nous servir de carreaux algébriques pour illustrer l’addition.
- Guidez les élèves à faire une soustraction d’entiers relatifs en tentant de résoudre le problème suivant : À 9 h, la température était de –3 °C. Trois heures plus tard, elle était de +2 °C. De combien de degrés a-t-elle augmenté au cours de cette période?
- Faites l’exercice d’addition et de soustraction d’entiers relatifs.
- Finalement, faites le rapprochement entre l’addition et la soustraction des entiers relatifs en leur montrant comment réécrire les équations.
Un carreau blanc représente un entier négatif.
Un carreau rouge représente un entier positif.
 |
Blanc (-) |  |
Rouge (+) |
Droite numérique horizontale
Sur une droite numérique horizontale, les nombres de gauche sont plus petits que ceux de droite.
Gagner 1 $ peut se représenter par +1.
Dépenser 1 $ peut se représenter par –1.
+1 et –1 sont ce qu’on appelle des nombres opposés. Ils sont équidistants de zéro sur la droite numérique.
La somme de deux entiers opposés est toujours zéro.
La somme de deux nombres opposés est égale à zéro. Autrement dit, c’est une somme nulle.
Exemple : (+1) + (–1) = 0
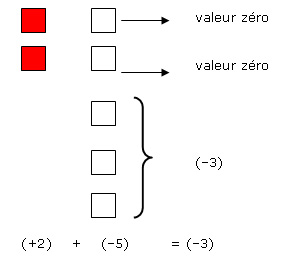
Nous pouvons utiliser des carreaux algébriques pour représenter la valeur zéro.


Gagner 2 $ est représenté par +2.
Dépenser 5 $ est représenté par –5.
(+2) + (–5) = ?
|
Nous pouvons illustrer la soustraction |
 |
||||||||||||||||
|
Comme nous avons (+2) ou 2 carreaux rouges, nous devons ajouter des valeurs zéro pour pouvoir soustraire (–3), soit 3 carreaux blancs. | ||||||||||||||||
| Addition de 3 valeurs zéro | |||||||||||||||||
Si nous enlevons (–3) ou 3 carreaux blancs, il nous reste 5 carreaux rouges ou (+5).
| (+2) | – | (-3) = (+5) | |
 |
 |
||
 |
 |
||
 |
|||
Informations pour l’enseignant
Les entiers positifs et négatifs peuvent être représentés par des différents objets, comme des carreaux qu’on appelle des carreaux algébriques.
Pour la soustraction des entiers relatifs, certains élèves trouveront plus facile d’ajouter à l’ensemble le nombre de « zéros » correspondant au deuxième terme de la soustraction, au lieu de calculer combien il leur en manque (ex. : -3 – -4 =). L’activité Exercices d’addition et de soustraction montre à l’élève qu’il doit ajouter une valeur de zéro pour pouvoir enlever 4 carreaux blancs. Il serait tout aussi bien d’ajouter 4 valeurs de zéro pour correspondre au -4 et de simplifier les valeurs de zéro restantes.
Source : Cartable Les entiers relatifs : Stratégies d’apprentissage favorisant une meilleure compréhension, Alberta Education, 2005.








