| Résultat(s) d’apprentissage : |
- 4e année, Le nombre, n° 9
|
| Description : |
Les élèves sont des détectives et utilisent leurs connaissances antérieures pour découvrir ce que signifie la virgule dans un nombre décimal. Les élèves sont mis devant une sélection de problèmes et cherchent un lien commun pour expliquer l’utilisation de la virgule dans un nombre. |
Activité
- Préparez les stations avec du vrai matériel ou à l’aide des sept indices.
- Divisez les élèves de la classe en petits groupes. Les groupes ne doivent pas être tous égaux, c'est-à-dire qu’il peut y avoir des élèves qui travaillent seuls, d’autres en équipe de 2 ou de 3. Expliquez-leur que vous avez reçu un message du détective M. Virgule. Lisez la note de M. Virgule. Il demande aux élèves de la classe de l’aider à expliquer la signification de l’utilisation d’une virgule dans un nombre. Montrez-leur la note.
- Indiquez les indices dans la classe. Munis d’une feuille pour prendre des notes et d’un crayon, permettez-leur d’aller lire, d’observer et de noter les indices qu’ils y découvrent.
- Les élèves circulent dans la classe. Ils observent, discutent entre eux et prennent des notes. Ils cherchent la signification de la virgule et la manière de représenter le nombre 3,6.
- Au fur et à mesure que les élèves ont fini de circuler, invitez-les à préparer une réponse au brouillon (car ils la partageront à l’oral) qu’ils aimeraient donner à M. Virgule.
- Partage en grand groupe des réponses. Il serait bon de rappeler aux élèves que toutes les observations qu’ils ont faites seront partagées et mises ensemble pour qu’on donne ensemble une réponse. Invitez les élèves à partager, à tour de rôle, une observation avec le groupe.
- Pour accélérer le processus et éviter beaucoup de répétition, demandez aux élèves s’ils ont fait la même observation que ce qui a été présenté. Si oui, notez l’observation et demandez-leur de marquer que cette observation est déjà mentionnée. Passons à la suivante.
- Amenez les élèves à placer le nombre 3, 6 entre 3 et 4. À partir de leurs connaissances des fractions, peuvent-ils noter le 3 et
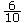 ? Observent-ils que toutes les stations constituent des exemples d’utilisation des nombres décimaux? Si un élève n’a pas mentionné qu’un nombre à virgule est un nombre décimal, il faudrait le mentionner. ? Observent-ils que toutes les stations constituent des exemples d’utilisation des nombres décimaux? Si un élève n’a pas mentionné qu’un nombre à virgule est un nombre décimal, il faudrait le mentionner.
- À partir des observations et des conclusions du groupe, écrivez une courte lettre de réponse à M. Virgule.
|
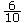 ? Observent-ils que toutes les stations constituent des exemples d’utilisation des nombres décimaux? Si un élève n’a pas mentionné qu’un nombre à virgule est un nombre décimal, il faudrait le mentionner.
? Observent-ils que toutes les stations constituent des exemples d’utilisation des nombres décimaux? Si un élève n’a pas mentionné qu’un nombre à virgule est un nombre décimal, il faudrait le mentionner.







